题目内容
已知函数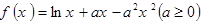 .
.
(1)若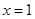 是函数
是函数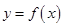 的极值点,求
的极值点,求 的值;
的值;
(2)求函数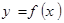 的单调区间.
的单调区间.
(1) ;(2)当
;(2)当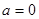 时,函数
时,函数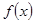 的单调递增区间为
的单调递增区间为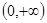 ;当
;当 时,函数
时,函数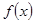 的单调递增区间是
的单调递增区间是 ,单调递减区间是
,单调递减区间是 。
。
解析试题分析:(1)先求函数的定义域,然后求导数,根据“若 是函数
是函数 的极值点,则
的极值点,则 是导数的零点”;(2)利用导数的正负分析原函数的单调性,按照列表分析.
是导数的零点”;(2)利用导数的正负分析原函数的单调性,按照列表分析.
试题解析:(1)函数定义域为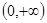 ,
, 2分
2分
因为 是函数
是函数 的极值点,所以
的极值点,所以
解得 或
或 4分
4分
经检验, 或
或 时,
时, 是函数
是函数 的极值点,
的极值点,
又因为a>0所以 6分
6分
(2)若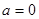 ,
,
所以函数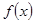 的单调递增区间为
的单调递增区间为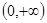 ;
;
若 ,令
,令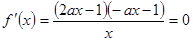 ,解得
,解得
当 时,
时, 的变化情况如下表
的变化情况如下表
所以函数




- 0 + 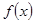

极大值 
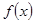 的单调递增区间是
的单调递增区间是 ,单调递减区间是
,单调递减区间是
考点:1.导数公式3.函数极值;3.函数的单调性.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 ,
,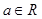 .
.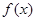 的单调性;
的单调性;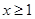 时,
时,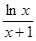 恒成立,求
恒成立,求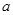 的取值范围.
的取值范围. (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式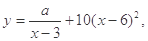 其中
其中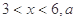 为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.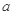 的值;
的值;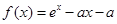 .
.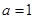 ,求
,求 的单调区间;
的单调区间;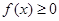 对一切
对一切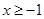 恒成立,求
恒成立,求 的取值范围.
的取值范围.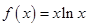 .
.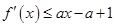 恒成立,求实数a的集合.
恒成立,求实数a的集合.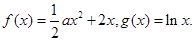 .
.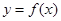 在区间
在区间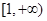 上是单调函数,求
上是单调函数,求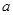 的取值范围;
的取值范围;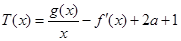 在区间
在区间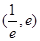 内有两个不同的零点(
内有两个不同的零点(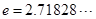 是自然对数的底数)?若存在,求出实数
是自然对数的底数)?若存在,求出实数
 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围.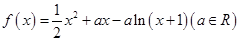 .
.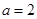 时,求函数
时,求函数 的极值;
的极值; ,
, 的单调性;
的单调性; ,则对于任意
,则对于任意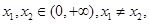 有
有 。
。