题目内容
下列结论正确的是______.(填序号)
(1)函数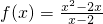 是奇函数
是奇函数
(2)函数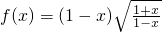 是偶函数
是偶函数
(3)函数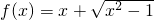 是非奇非偶函数
是非奇非偶函数
(4)函数f(x)=1既是奇函数又是偶函数.
解:对于(1),由于函数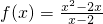 的定义域为{x|x≠2},定义域不关于原点对称,故函数是非奇非偶函数,故(1)不正确.
的定义域为{x|x≠2},定义域不关于原点对称,故函数是非奇非偶函数,故(1)不正确.
对于(2),由函数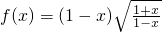 ,可得
,可得 ,求得的定义域为[-1,1),定义域不关于原点对称,故函数是非奇非偶函数,故(2)不正确.
,求得的定义域为[-1,1),定义域不关于原点对称,故函数是非奇非偶函数,故(2)不正确.
对于(3),由函数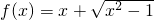 可得f(-x)=-x+
可得f(-x)=-x+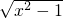 ≠±f(x),故函数f(x)是非奇非偶函数,故(3)正确.
≠±f(x),故函数f(x)是非奇非偶函数,故(3)正确.
对于(4),函数f(x)=1,∴f(-x)=1,故f(-x)=f(x),f(-x)≠-f(x) 故函数f(x)是偶函数,不是奇函数,故(4)不正确.
故答案为 (3).
分析:先看函数的定义域是否关于原点对称,再看f(-x)与f(x)的关系,再根据函数的奇偶性的定义作出判断.
点评:本题主要考查函数的奇偶性的判断方法,属于中档题.
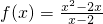 的定义域为{x|x≠2},定义域不关于原点对称,故函数是非奇非偶函数,故(1)不正确.
的定义域为{x|x≠2},定义域不关于原点对称,故函数是非奇非偶函数,故(1)不正确.对于(2),由函数
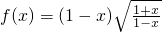 ,可得
,可得 ,求得的定义域为[-1,1),定义域不关于原点对称,故函数是非奇非偶函数,故(2)不正确.
,求得的定义域为[-1,1),定义域不关于原点对称,故函数是非奇非偶函数,故(2)不正确.对于(3),由函数
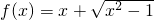 可得f(-x)=-x+
可得f(-x)=-x+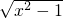 ≠±f(x),故函数f(x)是非奇非偶函数,故(3)正确.
≠±f(x),故函数f(x)是非奇非偶函数,故(3)正确.对于(4),函数f(x)=1,∴f(-x)=1,故f(-x)=f(x),f(-x)≠-f(x) 故函数f(x)是偶函数,不是奇函数,故(4)不正确.
故答案为 (3).
分析:先看函数的定义域是否关于原点对称,再看f(-x)与f(x)的关系,再根据函数的奇偶性的定义作出判断.
点评:本题主要考查函数的奇偶性的判断方法,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
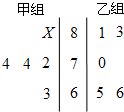 如图所示茎叶图记录了甲乙两组各5名同学的数学成绩.甲组成绩中有一个数据模糊,无法确认,在图中以X表示.若两个小组的平均成绩相同,则下列结论正确的是( )
如图所示茎叶图记录了甲乙两组各5名同学的数学成绩.甲组成绩中有一个数据模糊,无法确认,在图中以X表示.若两个小组的平均成绩相同,则下列结论正确的是( )| A、X=2,S甲2<S乙2 | B、X=2,S甲2>S乙2 | C、X=6,S甲2<S乙2 | D、X=6,2,S甲2>S乙2 |