题目内容
已知函数f（x）=alnx﹣ax﹣3（a∈R），函数f（x）的图象在x=4处的切线的斜率为
．
（1）求a值及函数f（x）的单调区间；
（2）若函数g（x）=
在区间（1，3）上不是单调函数（其中f′（x）是f（x）的导函数），求实数m的取值范围．
考点：
利用导数研究曲线上某点切线方程；函数的单调性与导数的关系．
专题：
导数的综合应用．
分析：
（1）先对函数求导，然后由由已知f'（4）=
，可求a．再求导数fˊ（x）然后在函数的定义域内解不等式fˊ（x）＞0和fˊ（x）＜0，fˊ（x）＞0的区间为单调增区间，fˊ（x）＜0的区间为单调减区间．
（2）由切线斜率为，可求出a值，进而求出f（x）、f′（x），因为g（x）在区间（1，3）上不单调，所以g′（x）改变符号，从而得到m所满足的条件．
解答：
解：（1）f（x）的定义域为（0，+∞），…（1分）
f'（x）=
…（2分）
由 f'（4）=﹣
= 得a=﹣2 …（4分）
所以f'（x）=
（x＞0）
由f'（x）＞0，得x＞1；f'（x）＜0，得0＜x＜1
所以f（x）的单增区间为（1，+∞），单减区间为（0，1]…（6分）
当a=﹣2时，若x∈（1，+∞），则f′（x）＞0；若x∈（0，1），则f′（x）＜0，
∴当a=﹣2时，f（x）的单调递增区间为[1，+∞），单调递减区间为（0，1]；
（2）g（x）=
…（7分）
g'（x）=x2+（m+4）x﹣2 …（8分）
因为g（x）在（1，3）不单调，且g'（0）=﹣2 …（9分）
所以 
…（11分）
即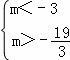 
…（12分）
所以m∈（﹣
，﹣3）．
点评：
本题考查了利用导数研究曲线上某点切线方程、导数与函数单调性的关系，利用导数解决问题的能力，注意数形结合思想的应用．
津桥教育计算小状元系列答案