题目内容
已知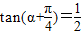 ,且
,且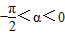 ,则
,则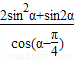 = .
= .
【答案】分析:由条件利用两角和的正切公式求出 tanα 的值,再由同角三角函数的基本关系求出sinα 的值,利用角函数的恒等变换化简
要求的式子为2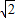 sinα,把sinα 的值代入运算求得结果.
sinα,把sinα 的值代入运算求得结果.
解答:解:∵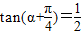 =
=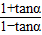 ,∴tanα=-
,∴tanα=- .
.
再由 tanα=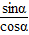 ,sin2α+cos2α=1,
,sin2α+cos2α=1,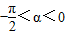 ,
,
可得 sinα=-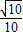 .
.
故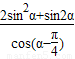 =
=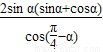 =
=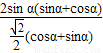 =2
=2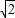 sinα
sinα
=2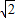 ×(-
×(-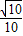 )=
)=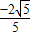 .
.
故答案为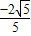 .
.
点评:本题主要考查三角函数的恒等变换及化简求值,注意角的范围及三角函数值的符号,这是解题的易错点.
要求的式子为2
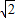 sinα,把sinα 的值代入运算求得结果.
sinα,把sinα 的值代入运算求得结果.解答:解:∵
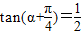 =
=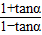 ,∴tanα=-
,∴tanα=- .
.再由 tanα=
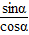 ,sin2α+cos2α=1,
,sin2α+cos2α=1,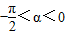 ,
,可得 sinα=-
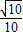 .
.故
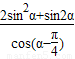 =
=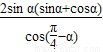 =
=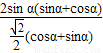 =2
=2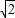 sinα
sinα =2
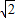 ×(-
×(-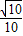 )=
)=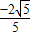 .
.故答案为
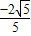 .
.点评:本题主要考查三角函数的恒等变换及化简求值,注意角的范围及三角函数值的符号,这是解题的易错点.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 、
、 且
且 ,则
,则 的取值范围为_______.
的取值范围为_______. 的前
的前 项和为
项和为 ,已知
,已知 ,且
,且 ,则
,则 (
)
(
) ,且
,且 ,则
,则 的值为 ;
的值为 ; ,且
,且 ,则
,则 的值为
的值为  ,且
,且 ,则集合M的个数是
,则集合M的个数是