题目内容
设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.(1)求数列{an}和{bn}的通项公式;
(2)设cn=![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
解:(1)当n=1时,a1=S1=2;
当n≥2时,an=Sn-Sn-1=2n2-2(n-1)2=4n-2.
故{an}的通项公式为an=4n-2,即{an}是a1=2,公差d=4的等差数列.
设{bn}的通项公式为q,则b1qd=b1,d=4,∴q=![]() .
.
故bn=b1qn-1-2×![]() ,即{bn}的通项公式为bn=
,即{bn}的通项公式为bn=![]() .
.
(2)∵cn=![]() =
=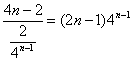 ,
,
∴Tn=c1+c2+…+cn=[1+3×41+5×42+…+(2n-1)4n-1],
4Tn=[1×4+3×42+5×43+…+(2n-3)4n-1+(2n-1)4n]
两式相减得
3Tn=-1-2(41+42+43+…+4n-1)+(2n-1)4n=![]() [(6n-5)4n+5],
[(6n-5)4n+5],
∴Tn=![]() [(6n-5)4n+5].
[(6n-5)4n+5].

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目