题目内容

已知集合A＝{x|log2(4x)·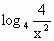≥2}，求函数y＝42x+1＋4x(x∈A)的值域．

答案：
解析：

 　　[解]由题意知(2＋log2x)(1－log2x)≥2，　　整理得 ＋log2x≤0，

　　[解]由题意知(2＋log2x)(1－log2x)≥2，　　整理得＋log2x≤0，

　　解不等式得　　－1≤log2x≤0，所以≤x≤1

　　令4x＝u，则u∈[2，4]

　　而函数y＝42x+1＋4x可化为　　y＝4u2＋u，u∈[2，4]．

　　又函数y＝4u2＋u在区间[2，4]上单调递增

　　故y≥4×22＋2＝18　　y≤4×42＋4＝68

　　函数y＝42x+1＋4x的值域为[18，68]．


练习册系列答案
相关题目
本题设有（1）（2）（3）三个选考题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
（1）已知矩阵M=
1a
b1
，N=
c2
0d
，且MN=
20
-20
，
（Ⅰ）求实数a，b，c，d的值；（Ⅱ）求直线y=3x在矩阵M所对应的线性变换下的像的方程．
（2）在直角坐标系xoy中，直线l的参数方程为
x=3-
2
2
t
y=
5
-
2
2
t
（t为参数）．在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为ρ=2
5
sinθ．
（Ⅰ）求圆C的直角坐标方程；（Ⅱ）设圆C与直线l交于点A、B，若点P的坐标为(3，
5
)，
求|PA|+|PB|．
（3）已知函数f（x）=|x-a|．
（Ⅰ）若不等式f（x）≤3的解集为{x|-1≤x≤5}，求实数a的值；
（Ⅱ）在（Ⅰ）的条件下，若f（x）+f（x+5）≥m对一切实数x恒成立，求实数m的取值范围．
本题设有（1）、（2）、（3）三个选考题，每题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分，作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
（1）选修4-2：矩阵与变换
设矩阵 M=
a0
0b
（其中a＞0，b＞0）．
（Ⅰ）若a=2，b=3，求矩阵M的逆矩阵M-1；
（Ⅱ）若曲线C：x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C′：
x2
4
+y2=1，求a，b的值．
（2）（本小题满分7分）选修4-4：坐标系与参数方程
在直接坐标系xOy中，直线l的方程为x-y+4=0，曲线C的参数方程为
x=
3
cos∂
y=sin∂
(∂为参数)．
（Ⅰ）已知在极坐标（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为（4，
π
2
），判断点P与直线l的位置关系；
（Ⅱ）设点Q是曲线C上的一个动点，求它到直线l的距离的最小值．
（3）（本小题满分7分）选修4-5：不等式选讲
设不等式|2x-1|＜1的解集为M．
（Ⅰ）求集合M；
（Ⅱ）若a，b∈M，试比较ab+1与a+b的大小．
本题（1）（2）（3）三个选答题，每小题5分，请考生任选1题作答，如果多做，则按所做的前1题计分．
（1）（选修4-1，几何证明选讲）如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB=AD=a，CD=
a
2
，点E，F分别为线段AB，CD的中点，则EF=
a
2
a
2
．
（2）（选修4-4，坐标系与参数方程）在极坐标系（ρ，θ）（0≤θ≤2π）中，曲线ρ=2sinθ与ρcosθ=-1的交点的极坐标为
（
2
，
3π
4
）
（
2
，
3π
4
）
．
（3）（选修4-1，不等式选讲）已知函数f（x）=|x-a|．若不等式f（x）≤3的解集为{x|-1≤x≤5}，则实数a的值为
a=2
a=2
．
本题共有（1）、（2）、（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多做，则以所做的前2题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
（1）选修4-2：矩阵与变换
变换T1是逆时针旋转90°的旋转变换，对应的变换矩阵为M1，变换T2对应的变换矩阵是M2=
11
01
；
（I）求点P（2，1）在T1作用下的点Q的坐标；
（II）求函数y=x2的图象依次在T1，T2变换的作用下所得的曲线方程．
（2）选修4-4：极坐标系与参数方程
从极点O作一直线与直线l：ρcosθ=4相交于M，在OM上取一点P，使得OM•OP=12．
（Ⅰ）求动点P的极坐标方程；
（Ⅱ）设R为l上的任意一点，试求RP的最小值．
（3）选修4-5：不等式选讲
已知f（x）=|6x+a|．
（Ⅰ）若不等式f（x）≥4的解集为{x|x≥
1
2
或x≤-
5
6
}，求实数a的值；
（Ⅱ）在（Ⅰ）的条件下，若f（x）+f（x-1）＞b对一切实数x恒成立，求实数b的取值范围．
选作题，本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
A．（几何证明选讲）
如图，已知两圆交于A、B两点，过点A、B的直线分别与两圆交于P、Q和M、N．求证：PM∥QN．
B．（矩阵与变换）
已知矩阵A的逆矩阵A-1=
10
02
，求矩阵A．
C．（极坐标与参数方程）
在平面直角坐标系xOy中，过椭圆
x2
12
+
y2
4
=1在第一象限处的一点P（x，y）分别作x轴、y轴的两条垂线，垂足分别为M、N，求矩形PMON周长最大值时点P的坐标．
D．（不等式选讲）
已知关于x的不等式|x-a|+1-x＞0的解集为R，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网