题目内容
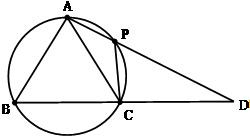在△ABC中，AB=AC，过点A的直线与其外接圆交于点P，交BC延长线于点D．（1）求证：
| PC |
| AC |
| PD |
| BD |
（2）若AC=3，求AP•AD的值．
分析：（1）先由角相等∠CPD=∠ABC，∠D=∠D，证得三角形相似，再结合线段相等即得所证比例式；
（2）由于∠ACD=∠APC，∠CAP=∠CAP，从而得出两个三角形相似：“△APC～△ACD”结合相似三角形的对应边成比例即得AP•AD的值．
（2）由于∠ACD=∠APC，∠CAP=∠CAP，从而得出两个三角形相似：“△APC～△ACD”结合相似三角形的对应边成比例即得AP•AD的值．
解答：解：（1）∵∠CPD=∠ABC，∠D=∠D，
∴△DPC～△DBA，∴
=
又∵AB=AC，∴
=
（5分）
（2）∵∠ACD=∠APC，∠CAP=∠CAP，∴△APC～△ACD∴
=
，
∴AC2=AP•AD=9（5分）
∴△DPC～△DBA，∴
| PC |
| AB |
| PD |
| BD |
又∵AB=AC，∴
| PC |
| AC |
| PD |
| BD |
（2）∵∠ACD=∠APC，∠CAP=∠CAP，∴△APC～△ACD∴
| AP |
| AC |
| AC |
| AD |
∴AC2=AP•AD=9（5分）
点评：本小题属于基础题．此题主要考查的是相似三角形的性质、相似三角形的判定，正确的判断出相似三角形的对应边和对应角是解答此题的关键．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目