题目内容
某网站体育版块足球栏目组发起了“射手的连续进球与射手在场上的区域位置有关系”的调查活动,在所有参与调查的人中,持“有关系”“无关系”“不知道”态度的人数如表所示:
| | 有关系 | 无关系 | 不知道 |
| 40岁以下 | 800 | 450 | 200 |
| 40岁以上(含40岁) | 100 | 150 | 300 |
(2)在持“不知道”态度的人中,用分层抽样的方法抽取10人看作一个总体.①从这10人中选取3人,求至少一人在40岁以下的概率;②从这10人中人选取3人,若设40岁以下的人数为X,求X的分布列和数学期望.
(1)100;(2)① ;②
;② .
.
解析试题分析:
解题思路:(1)根据分层抽样的特点“等比例抽样”求解即可;(2)①利用古典概型概率公式以及对立事件概率公式求解;②利用超几何分布的概率公式求概率,再求期望即可.
规律总结:1.遇到“至少”、“至多”,且正面情况较多时,可以考虑对立事件的概率;2.利用概率或随机变量的分布列以及期望、方差解决应用题时,要注意随机变量的实际意义.
试题解析:(1)由题意,得
∴n=100
(2)设所选取的人中有m人在40岁以下
则 ,解得m=4
,解得m=4
①记“至少一人在40岁以下”为事件A
则
②X的可能取值为0,1,2,3



∴x的分布列为X 0 1 2 3 P 



 .
.
考点:1.分层抽样;2.超几何分布;3.离散型随机变量的分布列与期望.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
处罚金额 (元) (元) | 0 | 5 | 10 | 15 | 20 |
会闯红灯的人数 | 80 | 50 | 40 | 20 | 10 |
(Ⅰ)求这两种金额之和不低于20元的概率;
(Ⅱ)若用X表示这两种金额之和,求X的分布列和数学期望.
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下
| | 男 | 女 | 合计 |
| 需要 | 40 | 30 | |
| 不需要 | 160 | 270 | |
| 合计 | | | |
(2)能否在犯错误的概率不超过0.01的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关系?
(3)根据(2)的结论,能否提出更好的调查方法估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由。
附表:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
| 年份 | 2004 | 2006 | 2008 | 2010 | 2012 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
(1)利用所给数据求年需求量与年份之间的回归直线方程
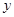 =
= x+
x+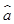
(2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量.
某车间加工零件的数量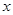 与加工时间
与加工时间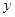 的统计数据如表:
的统计数据如表:
零件数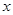 (个) (个) | 10 | 20 | 30 |
加工时间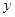 (分钟) (分钟) | 21 | 30 | 39 |
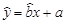 中的
中的 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )A.112分钟 B.102分钟 C.94分钟 D.84分钟

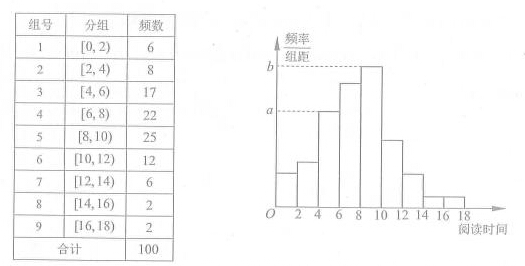
 元的同学有30人,则n的值为 。
元的同学有30人,则n的值为 。