Question

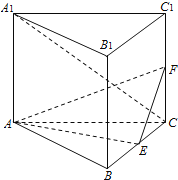
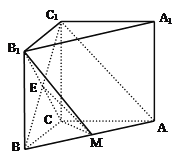
【题目】如图，直三棱柱中，，，点在线段上.

（1）若是中点，证明：平面；

（2）当长是多少时，三棱锥的体积是三棱柱的体积的.

Answer 1

【答案】（1）详见解析（2）

【解析】

试题分析：（1）证明线面平行，一般利用线面平行判定定理，即从线线平行出发给予证明，而线线平行的寻找与论证，往往需要结合平几知识，如本题利用三角形中位线性质得线线平行（2）求三棱锥体积，关键是确定其高，而本题为直三棱柱，因此，而，所以体积比等于,解得

试题解析：（Ⅰ）证明：连结BC1，交B1C于E，连结ME．

因为 直三棱柱ABC-A1B1C1，M是AB中点，所以侧面BB1C1C为矩形，

ME为△ABC1的中位线，所以ME//AC1．

因为ME平面B1CM，AC1平面B1CM，所以AC1∥平面B1CM

（II），

设，

故，即

故当时，

三棱锥的体积是三棱柱的体积的.