题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,向量 =(sinA,b+c),
=(sinA,b+c), =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足 ⊥
⊥ ,则角B=
,则角B=
- A.

- B.

- C.

- D.

B
分析:由题意可得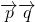 =0,应用正弦定理、余弦定理 可得cosB=
=0,应用正弦定理、余弦定理 可得cosB= =
= ,又 0<B<π,可得
,又 0<B<π,可得
B= .
.
解答:由题意可得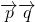 =(a-c)sinA+(b+c)(sinC-sinB)=2r[sin2A-sinAsinC]
=(a-c)sinA+(b+c)(sinC-sinB)=2r[sin2A-sinAsinC]
+2r[sinB sinC-sin2B+sin2C-sinCsinB]=2r[sin2A+sin2C-sin2B-sinAsinC]=0.
∴sin2A+sin2C-sin2B=sinAsinC,∴a2+c2-b2=ac.
∴cosB= =
= ,又 0<B<π,B=
,又 0<B<π,B= ,
,
故选 B.
点评:本题考查两个向量的数量积公式的应用,两个向量垂直的性质,正弦定理、余弦定理的应用,得到 cosB= =
= ,是解题的关键.
,是解题的关键.
分析:由题意可得
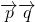 =0,应用正弦定理、余弦定理 可得cosB=
=0,应用正弦定理、余弦定理 可得cosB= =
= ,又 0<B<π,可得
,又 0<B<π,可得B=
 .
.解答:由题意可得
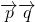 =(a-c)sinA+(b+c)(sinC-sinB)=2r[sin2A-sinAsinC]
=(a-c)sinA+(b+c)(sinC-sinB)=2r[sin2A-sinAsinC]+2r[sinB sinC-sin2B+sin2C-sinCsinB]=2r[sin2A+sin2C-sin2B-sinAsinC]=0.
∴sin2A+sin2C-sin2B=sinAsinC,∴a2+c2-b2=ac.
∴cosB=
 =
= ,又 0<B<π,B=
,又 0<B<π,B= ,
,故选 B.
点评:本题考查两个向量的数量积公式的应用,两个向量垂直的性质,正弦定理、余弦定理的应用,得到 cosB=
 =
= ,是解题的关键.
,是解题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |