题目内容
已知7件产品中有2件次品,现逐一不放回地进行检验,直到2件次品都能被确认为止.(I)求检验次数为4的概率;
(II)设检验次数为ξ,求ξ的分布列和数学期望.
【答案】分析:(I)检验次数为4的情况是前3次在5件正品中取到2件,在2件次品中取到1件,第4次取到次品,由此能求出检验次数为4的概率.
(II)ξ的可能值为2,3,4,5,6,P(ξ=2)=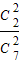 =
=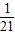 ,P(ξ=3)=
,P(ξ=3)=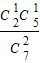 •
•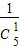 =
=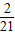 ,P(ξ=4)=
,P(ξ=4)= ,
,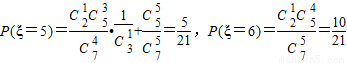 .由此能求出ξ的分布列和ξ的期望.
.由此能求出ξ的分布列和ξ的期望.
解答:解:(I)记“在4次检验中,前3次检验中有1次得到次品,第4次检验得到次品”为事件A,则检验次数为4的概率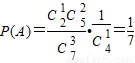 .…(3分)
.…(3分)
(II)ξ的可能值为2,3,4,5,6,其中P(ξ=2)=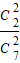 =
=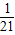 ,
,
P(ξ=3)=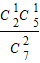 •
•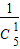 =
=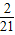 ,
,
P(ξ=4)= ,
,
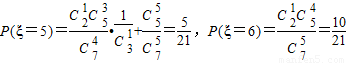 .…(8分)
.…(8分)
∴ξ的分布列为
…(10分)
ξ的期望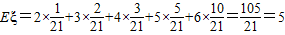 …(12分)
…(12分)
点评:本题考查概率的求法和离散型随机变量的概率分布列和数学期望.解题时要认真审题,注意概率的性质和排列组合数公式的运用.
(II)ξ的可能值为2,3,4,5,6,P(ξ=2)=
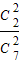 =
=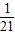 ,P(ξ=3)=
,P(ξ=3)=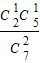 •
•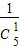 =
=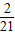 ,P(ξ=4)=
,P(ξ=4)= ,
,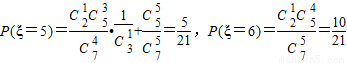 .由此能求出ξ的分布列和ξ的期望.
.由此能求出ξ的分布列和ξ的期望.解答:解:(I)记“在4次检验中,前3次检验中有1次得到次品,第4次检验得到次品”为事件A,则检验次数为4的概率
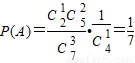 .…(3分)
.…(3分)(II)ξ的可能值为2,3,4,5,6,其中P(ξ=2)=
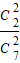 =
=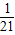 ,
,P(ξ=3)=
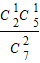 •
•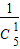 =
=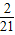 ,
,P(ξ=4)=
 ,
,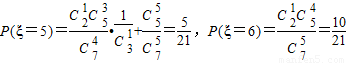 .…(8分)
.…(8分)∴ξ的分布列为
| ξ | 2 | 3 | 4 | 5 | 6 |
| P | 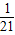 | 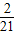 |  | 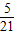 | 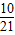 |
ξ的期望
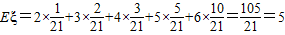 …(12分)
…(12分)点评:本题考查概率的求法和离散型随机变量的概率分布列和数学期望.解题时要认真审题,注意概率的性质和排列组合数公式的运用.

练习册系列答案
相关题目