Question

已知曲线W上的动点M到点F（1，0）的距离等于它到直线x=-1的距离．过点P（-1，0）任作一条直线l与曲线W交于不同的两点A、B，点A关于x轴的对称点为C．
（Ⅰ）求曲线W的方程；
（Ⅱ）求证

FC

=λ

FB

(λ∈R)；
（Ⅲ）求△PBC面积S的取值范围．

Answer 1

分析：（Ⅰ）由题知，曲线W是以F（1，0）为焦点，以直线x=-1准线的抛物线，由此可求出曲线W的方程．
（Ⅱ）因为直线l与曲线W交于A、B两点，所以l的斜率k存在，设直线l的方程为y=k（x+1），

y=k(x+1) y2=4x

得，k²x²+（2k²-4）x+k²=0．再由根的判别式和根与系数的关系进行求解．
（Ⅲ）由题意S=

1

2

|PF|•|y1+y2|=|k（x₁+x₂+2）|=|k(

4-2k2

k2

+2)|=

4

|k|

，再由|k|＜1且k≠0，可以求出S的取值范围．

解答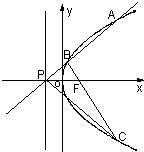：解：（Ⅰ）由题知，曲线W是以F（1，0）为焦点，以直线x=-1准线的抛物线，
所以曲线W的方程为y²=4x．（2分）
（Ⅱ）因为直线l与曲线W交于A、B两点，所以l的斜率k存在，且k≠0
设直线l的方程为y=k（x+1），

y=k(x+1) y2=4x

得，k²x²+（2k²-4）x+k²=0．（4分）
因为直线l与曲线W交于A、B两点，
所以k≠0，△=4（k²-2）²-4k⁴＞0，即|k|＜1且k≠0．
设点A，B的坐标分别为（x₁，y₁），（x₂，y₂），
则x1+x2=

4-2k2

k2

，x₁x₂=1，点C的坐标为（x₁，-y₁），y₁=k（x₁+1），y₂=k（x₂+1）．
所以

FC

=(x1-1，-y1)，

FB

=(x2-1，y2)．（8分）
又因为（x₁-1）y₂-（x₂-1）（-y₁）
=（x₁-1）k（x₂+1）+（x₂-1）k（x₁+1）
=k（2x₁x₂-2）=0，
所以

FC

=λ

FB

．（10分）
（Ⅲ）由题意S=

1

2

|PF|•|y1+y2|（12分）
=|k（x₁+x₂+2）|
=|k(

4-2k2

k2

+2)|
=

4

|k|

．（13分）
因为|k|＜1且k≠0，所以S的取值范围是（4，+∞）．（14分）

点评：本题考查圆锥曲线和直线的位置关系和应用，解题时要认真审题，注意根的判别式和根与系数的关系的合理运用．