题目内容
函数f（x）的图象如图所示，f'（x）是函数f（x）的导函数，则下列排序正确的是
- A.f'（3）＜f'（1）＜f（3）-f（1）＜0
- B.
- C.
- D.f'（3）＜f（3）-f（1）＜f'（1）＜0
C
分析：根据f（x）的图象可知，函数在（0，+∞）单调递减，得到f′（x）小于0且导函数为增函数，再根据中值定理得到在（1，3）存在一点ξ，f′（ξ）成立，利用增减性找到正确的选项即可．
解答：由函数图象知，f（x）在（0，+∞）单调递减，所以f′（x）＜0；且f′（x）为增函数；
根据中值定理得到在（1，3）存在一点ξ，
f′（ξ）=
，所以
故选C．
点评：考查学生利用导数研究函数的单调性的能力，以及会利用中值定理解决数学问题的能力．
分析：根据f（x）的图象可知，函数在（0，+∞）单调递减，得到f′（x）小于0且导函数为增函数，再根据中值定理得到在（1，3）存在一点ξ，f′（ξ）成立，利用增减性找到正确的选项即可．
解答：由函数图象知，f（x）在（0，+∞）单调递减，所以f′（x）＜0；且f′（x）为增函数；
根据中值定理得到在（1，3）存在一点ξ，
f′（ξ）=
，所以故选C．
点评：考查学生利用导数研究函数的单调性的能力，以及会利用中值定理解决数学问题的能力．
练习册系列答案
相关题目
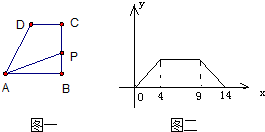直角梯形ABCD中，∠B=90°，动点P从点B出发，沿B→C→D→A的路线运动，设点P运动的路程为x，△APB的面积为f（x），若函数f（x）的图象如图所示，则△ABC的面积为（ ）
函数f（x）的图象如图，f′（x）是f（x）的导函数，则下列数值排列正确的是（ ）
已知f（x）是定义域为R的奇函数，f（-4）=-2，f（x）的导函数f′（x）的图象如图所示，若两正数a，b满足f（a+2b）＜2，则
（2012•开封一模）函数f（x）满足f（0）=0，其导函数f′（x）的图象如图，则f（x）的图象与x轴所围成的封闭图形的面积为（ ）
函数f（x）满足f（0）=0，其导函数f'（x）的图象如图，则f（x）在[-2，1]上的最小值为（ ）