题目内容
已知三角形△ABC三内角满足A、B、C成等差数列，tanAtanC=2+
，又顶点C对边c上的高等于4
，求三角形三边a、b、c的长．
| 3 |
| 3 |
由A+B+C=180°及A+C=2B，
得B=60°，A+C=120°，…（2分）
∴tan(A+C)=
=-
，又tanAtanC=2+
，
∴tanA+tanC=3+
，…（4分）
∴tanA，tanC为二次方程x2-（3+
）x+2+
=0的根，
∴tanA=1，tanA=2+
或tanC=2+
，tanC=1，
∴A=45°，C=75°或A=75°，C=45°，…（8分）
①若A=45°，C=75°，则B=60°，
根据正弦定理
=
，
=
，
=
，
则a=
=8，b=
=4
，c=
=4(
+1)；…（10分）
②若A=75°，C=45°，则B=60°，同理可得：
a=8，b=4（3
-
），c=8（
-1）．…（12分）
得B=60°，A+C=120°，…（2分）
∴tan(A+C)=
| tanA+tanC |
| 1-tanAtanC |
| 3 |
| 3 |
∴tanA+tanC=3+
| 3 |
∴tanA，tanC为二次方程x2-（3+
| 3 |
| 3 |
∴tanA=1，tanA=2+
| 3 |
| 3 |
∴A=45°，C=75°或A=75°，C=45°，…（8分）
①若A=45°，C=75°，则B=60°，
根据正弦定理
| a |
| sin90° |
| h |
| sin60° |
| b |
| sin90° |
| h |
| sin45° |
| c |
| sinC |
| a |
| sinA |
则a=
4
| ||
| sin60° |
4
| ||
| sin45° |
| 6 |
| asinc |
| sinA |
| 3 |
②若A=75°，C=45°，则B=60°，同理可得：
a=8，b=4（3
| 2 |
| 6 |
| 3 |
练习册系列答案
相关题目
，又顶点C对边c上的高等于4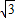
，求三角形三边a、b、c的长．