题目内容
设函数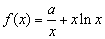 ,
, 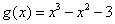 .
.
(Ⅰ)讨论函数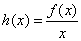 的单调性;
的单调性;
(Ⅱ)如果存在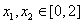 ,使得
,使得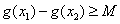 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数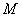 ;
;
(Ⅲ)如果对任意的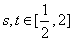 ,都有
,都有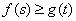 成立,求实数
成立,求实数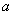 的取值范围.
的取值范围.
解:(Ⅰ) ,
, ,
,
① ,函数
,函数 在
在 上单调递增
上单调递增
② ,
, ,函数
,函数 的单调递增区间为
的单调递增区间为
 ,函数
,函数 的单调递减区间为
的单调递减区间为 .
.
(Ⅱ)存在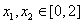 ,使得
,使得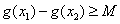 成立
成立
等价于: ,
,
考察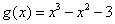 ,
,  ,
,
|
|
|
|
|
|
|
|
|
| 递减 | 极(最)小值 | 递增 |
|
.
由上表可知: ,
,
 ,
,
所以满足条件的最大整数 ;
;
(Ⅲ)问题等价于当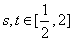 ,
, ,
,
即当 时,
时, 恒成立,
恒成立,
等价于 恒成立,
恒成立,
记 ,所以
,所以
 ,
,  。
。
记 ,当
,当 ,
,
即函数 在区间
在区间 上递增,
上递增,
当 ,
, ,即函数
,即函数 在区间
在区间 上递减,
上递减,
 取到极大值也是最大值
取到极大值也是最大值 所以
所以 。
。
另解:设 ,
, ,
,
∵ ,
, ,∴
,∴ 在
在 上递减,
上递减,
且 ,∴当
,∴当 时,
时, ,
, 时,
时, ,
,
即函数 在区间
在区间 上递增,在区间
上递增,在区间 上递减,
上递减,
所以 ,所以
,所以 。
。

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目










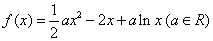
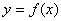 存在极大值和极小值,求
存在极大值和极小值,求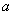 的取值范围;
的取值范围;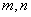 分别为
分别为 的极大值和极小值,其中
的极大值和极小值,其中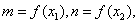 且
且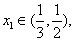 求
求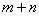 的取值范围.
的取值范围.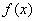 是定义在
是定义在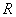 上的奇函数,当
上的奇函数,当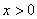 时,
时,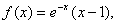 给出以下命题:
给出以下命题:
 时,
时,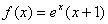 ; ②函数
; ②函数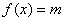 有解,则实数
有解,则实数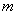 的取值范围是
的取值范围是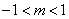 ;
;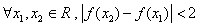 恒成立.
恒成立.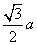 ,类比上述命题,棱长为
,类比上述命题,棱长为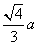 B.
B. C.
C. D.
D.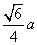
 ,其导函数为
,其导函数为 。
。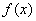 在
在 处的切线
处的切线 的方程
的方程 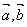 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么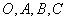 为空间四点,且向量
为空间四点,且向量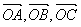 不构成空间的一个基底,则点
不构成空间的一个基底,则点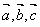 是空间的一个基底,则向量
是空间的一个基底,则向量 也是空间的一个基底其中正确的命题是 ( )
也是空间的一个基底其中正确的命题是 ( ) 的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率
的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率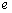 为 ( )
为 ( )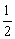 (B)
(B) 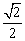 (C)
(C)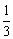 (D)
(D)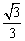
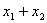 =6,
=6, = ( )
= ( )  的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.