题目内容
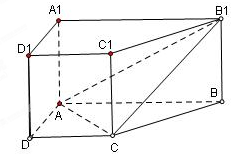
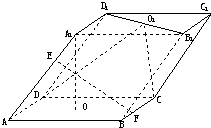
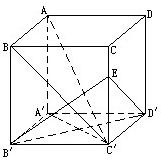
在长方体AC′中，AB=AC=a，BB′=b（b＞a），连接BC′，过点B′作B′E⊥BC′交CC′于E．
（1）求证：AC′⊥平面EB′D′；
（2）求三棱锥C′-B′D′E的体积．
（1）求证：AC′⊥平面EB′D′；
（2）求三棱锥C′-B′D′E的体积．
（1）证明：由题意，长方体底面为正方形，
A′C′⊥B′D′，AC′⊥B′D′，
又∵B′E⊥BC′，
∴AC′⊥B′E，
∴AC′⊥平面EB′D′
（2）由∠B′C′B=∠B′EC′，又EC′=
=
．
∴VC′-B′D′E=VE-B′C′D′=
×
a2×
=
A′C′⊥B′D′，AC′⊥B′D′，
又∵B′E⊥BC′，
∴AC′⊥B′E，
∴AC′⊥平面EB′D′
（2）由∠B′C′B=∠B′EC′，又EC′=
| a |
| tan∠B′EC′ |
| a2 |
| b |
∴VC′-B′D′E=VE-B′C′D′=
| 1 |
| 3 |
| 1 |
| 2 |
| a2 |
| b |
| a4 |
| 6b |
练习册系列答案
相关题目
