题目内容
在有限数列{an}中，Sn是{an}的前n项和，若把
称为数列{an}的“优化和”，现有一个共2010项的数列{an}：a1，a2，a3，…，a2010，若其“优化和”为2011，则有2011项的数列1，a1，a2，a3，…，a2010的“优化和”为（ ）A．2009
B．2010
C．2011
D．2012
【答案】分析：首先根据定义得出S1+S2+…+S2010=2010×2011，然后根据S1=a1，S2=a1+a2，…S2010=a1+a2+a3+…a2010，即可求出结果．
解答：解：∵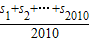
=2011∴S1+S2+…+S2010=2010×2011，
其中S1=a1，S2=a1+a2，…S2010=a1+a2+a3+…a2010．
∴所求的优化和=[1+（1+a1）+（1+a1+a2）+…+（1+a1+…+a2009）+（1+a1+…+a2010）]÷2011=[1+（ 1+S1）+（1+S2）+…+（1+S2009）+（1+S2010）]÷2011=[2011×1+（S1+S2+…+S2010）]÷2011=[2011+2010×2011]÷2011=1+2010=2011
故选C．
点评：本题考差了数列的求和，解题的关键是正确理解新定义，得出
=2011，属于中档题．
解答：解：∵
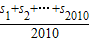=2011∴S1+S2+…+S2010=2010×2011，其中S1=a1，S2=a1+a2，…S2010=a1+a2+a3+…a2010．
∴所求的优化和=[1+（1+a1）+（1+a1+a2）+…+（1+a1+…+a2009）+（1+a1+…+a2010）]÷2011=[1+（ 1+S1）+（1+S2）+…+（1+S2009）+（1+S2010）]÷2011=[2011×1+（S1+S2+…+S2010）]÷2011=[2011+2010×2011]÷2011=1+2010=2011
故选C．
点评：本题考差了数列的求和，解题的关键是正确理解新定义，得出
=2011，属于中档题． 
练习册系列答案
高中必刷题系列答案
相关题目
称为数列{an}的“优化和”，现有一个共2006项的数列{an}：a1，a2，a3，…，a2006，若其“优化和”为2007，则有2007项的数列1，a1，a2，a3，…，a2006的“优化和”为（ ）
称为数列{an}的“均和”.现有一个共2010项的数列{an}：a1，a2，a3，…，a2009，a2010若其“均和”为2011，则有2011项的数列1，a1，a2，a3，…，a2009，a2010的“均和”为 .
称为数列{an}的“优化和”，现有一个共2006项的数列{an}：a1，a2，a3，…，a2006，若其“优化和”为2007，则有2007项的数列1，a1，a2，a3，…，a2006的“优化和”为 （ ）