题目内容
(2012•太原模拟)某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图:
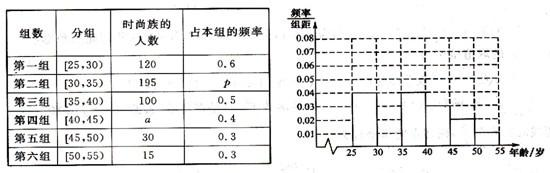
完成以下问题:
(Ⅰ)补全频率分布直方图并求n,a,p的值;
(Ⅱ)从[40,50)岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和期望E(X)..

完成以下问题:
(Ⅰ)补全频率分布直方图并求n,a,p的值;
(Ⅱ)从[40,50)岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和期望E(X)..
分析:(Ⅰ)根据所求矩形的面积和为1求出第二组的频率,然后求出高,画出频率直方图,求出第一组的人数和频率从而求出n,由题可知,第二组的频率以及人数,从而求出p的值,然后求出第四组的频率和人数从而求出a的值;
(Ⅱ)因为[40,45)岁年龄段的“时尚族”与[45,50)岁年龄段的“时尚族”的比值为2:1,所以采用分层抽样法抽取18人,[40,45)岁中有12人,[45,50)岁中有6人,机变量X服从超几何分布,X的取值可能为0,1,2,3,分别求出相应的概率,列出分布列,根据数学期望公式求出期望即可.
(Ⅱ)因为[40,45)岁年龄段的“时尚族”与[45,50)岁年龄段的“时尚族”的比值为2:1,所以采用分层抽样法抽取18人,[40,45)岁中有12人,[45,50)岁中有6人,机变量X服从超几何分布,X的取值可能为0,1,2,3,分别求出相应的概率,列出分布列,根据数学期望公式求出期望即可.
解答:解:(Ⅰ)第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,
所以高为
=0.06.
频率直方图如下:
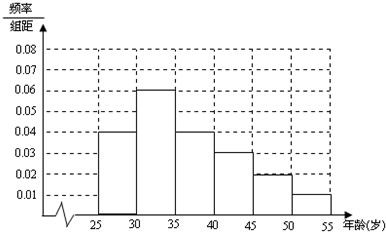
(2分)
第一组的人数为
=200,频率为0.04×5=0.2,所以n=
=1000.
由题可知,第二组的频率为0.3,所以第二组的人数为1000×0.3=300,
所以p=
=0.65.
第四组的频率为0.03×5=0.15,所以第四组的人数为1000×0.15=150,
所以a=150×0.4=60.(5分)
(Ⅱ)因为[40,45)岁年龄段的“时尚族”与[45,50)岁年龄段的“时尚族”的比值
为60:30=2:1,所以采用分层抽样法抽取18人,[40,45)岁中有12人,[45,50)岁中有6人.(6分)
随机变量X服从超几何分布.P(X=0)=
=
,P(X=1)=
=
,P(X=2)=
=
,P(X=3)=
=
.
所以随机变量X的分布列为
(10分)
∴数学期望EX=0×
+1×
+2×
+3×
=2
(或者 EX=
=2).(12分)
所以高为
| 0.3 |
| 5 |
频率直方图如下:

(2分)
第一组的人数为
| 120 |
| 0.6 |
| 200 |
| 0.2 |
由题可知,第二组的频率为0.3,所以第二组的人数为1000×0.3=300,
所以p=
| 195 |
| 300 |
第四组的频率为0.03×5=0.15,所以第四组的人数为1000×0.15=150,
所以a=150×0.4=60.(5分)
(Ⅱ)因为[40,45)岁年龄段的“时尚族”与[45,50)岁年龄段的“时尚族”的比值
为60:30=2:1,所以采用分层抽样法抽取18人,[40,45)岁中有12人,[45,50)岁中有6人.(6分)
随机变量X服从超几何分布.P(X=0)=
| ||||
|
| 5 |
| 204 |
| ||||
|
| 15 |
| 68 |
| ||||
|
| 33 |
| 68 |
| ||||
|
| 55 |
| 204 |
所以随机变量X的分布列为
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
∴数学期望EX=0×
| 5 |
| 204 |
| 15 |
| 68 |
| 33 |
| 68 |
| 55 |
| 204 |
(或者 EX=
| 12×3 |
| 18 |
点评:本题主要考查了频率分布直方图,离散型随机变量的分布列和数学期望,同时考查了超几何分布的概念和计算能力,属于中档题.

练习册系列答案
相关题目
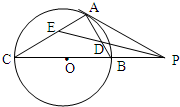 (2012•太原模拟)选修4-1:几何证明选讲
(2012•太原模拟)选修4-1:几何证明选讲