题目内容
已知函数f(x)=ex-1(e是自然对数的底数).
(1)证明:对任意的实数x,不等式f(x)≥x恒成立;
(2)数列{ }(n∈N+)的前n项和为Tn,求证:Tn<
}(n∈N+)的前n项和为Tn,求证:Tn<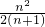 .
.
解:(I)设h(x)=f(x)-x=ex-1-x
∴h'(x)=ex-1-1,
当x>1时,h'(x)>0,h(x)为增,
当x<1时,h'(x)<0,h(x)为减,
当x=1时,h(x)取最小值h(1)=0.
∴h(x)≥h(1)=0,即f(x)≥x
(II)由(I)可知,对任意的实数x,不等式ex-1≥x恒成立,
所以 ,ln
,ln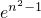 ≥lnn2,即n2-1≥lnn2,
≥lnn2,即n2-1≥lnn2,
 ,
,
 =
=

<
= =
= =
=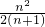
分析:(1)对函数h(x)=f(x)-x进行求导,通过判断函数h(x)的增减性求出其最小值大于等于0即可.
(2)由(1)可得不等式ex-1≥x成立,转化可得 ,表示出Tn将
,表示出Tn将 代入即可得到答案.
代入即可得到答案.
点评:本题主要考查通过求函数的导数来判断函数的单调性问题.还考查不等式的转化问题.
∴h'(x)=ex-1-1,
当x>1时,h'(x)>0,h(x)为增,
当x<1时,h'(x)<0,h(x)为减,
当x=1时,h(x)取最小值h(1)=0.
∴h(x)≥h(1)=0,即f(x)≥x
(II)由(I)可知,对任意的实数x,不等式ex-1≥x恒成立,
所以
 ,ln
,ln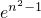 ≥lnn2,即n2-1≥lnn2,
≥lnn2,即n2-1≥lnn2, ,
, =
=

<

=
 =
= =
=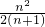
分析:(1)对函数h(x)=f(x)-x进行求导,通过判断函数h(x)的增减性求出其最小值大于等于0即可.
(2)由(1)可得不等式ex-1≥x成立,转化可得
 ,表示出Tn将
,表示出Tn将 代入即可得到答案.
代入即可得到答案.点评:本题主要考查通过求函数的导数来判断函数的单调性问题.还考查不等式的转化问题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目