Question

在等差数列{a_n}和等比数列{b_n}中,已知a₁=b₁=1,a₂=b₂≠1,a₈=b₃,

(1)求数列{a_n}的公差和数列{b_n}的公比.

(2)是否存在常数x、y,使得对于一切正整数n,都有a_n=log_xb_n+y成立?若存在,求出x和y;若不存在,请说明理由.

Answer 1

解:(1)设等差数列的公差为d,等比数列的公比为q,则

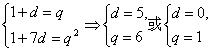 (舍).

(2)假设存在x、y,使得a_n=log_xb_n+y成立(n∈N^*),

即1+(n-1)×5=log_x6^n-1+y,

所以5n-4=(n-1)log_x6+y.

(5-log_x6)n-(4+y-log_x6)=0对一切正整数n都成立,所以

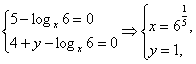
即存在常数x= ,y=1,使得对于一切正整数n,都有a_n=log_xb_n+y成立.