题目内容
数列 的前n项和记为
的前n项和记为 ,点(n,
,点(n, )在曲线
)在曲线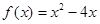 (
(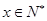 )上
)上
(1)求数列 的通项公式;
的通项公式;
(2)设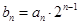 ,求数列
,求数列 的前n项和
的前n项和 的值.
的值.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由 与
与 满足的关系式,由
满足的关系式,由 可求得
可求得 的通项公式;(2)由一个等差数列和一个等比数列的乘积采用错位相减法求和的方法求数列
的通项公式;(2)由一个等差数列和一个等比数列的乘积采用错位相减法求和的方法求数列 的和.
的和.
试题解析:(1)由条件得 (
( )
)
当

当 也适合
也适合
所以通项公式为: .
.
(2)、
2
两式相减得,
解得
考点:(1)由 的表达式求数列
的表达式求数列 的通项公式;(2)错位相减求和.
的通项公式;(2)错位相减求和.

练习册系列答案
相关题目
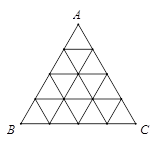
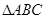 分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点
分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点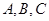 处的三个数互不相同且和为1,则所有顶点的数之和
处的三个数互不相同且和为1,则所有顶点的数之和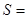 .
.
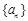 中,如果对任意的
中,如果对任意的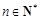 ,都有
,都有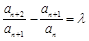 (
(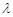 为常数),则称数列
为常数),则称数列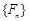 满足
满足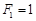 ,
,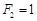 ,
,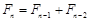 (
(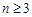 ),则该数列不是比等差数列;②若数列
),则该数列不是比等差数列;②若数列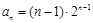 ,则数列
,则数列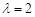 ;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若
;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若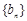 是等比数列,则数列
是等比数列,则数列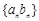 是比等差数列.
是比等差数列. ,各项均为正数的数列
,各项均为正数的数列 满足
满足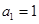 ,
,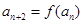 ,若
,若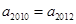 ,则
,则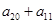 的值是 .
的值是 .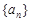 的前
的前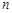 项和为
项和为 ,且
,且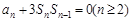 ,
,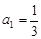 .
.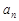 ;
;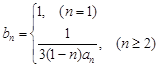 ,设
,设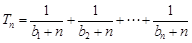 ,若
,若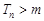 对
对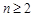 恒成立,求实数
恒成立,求实数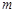 的取值范围.
的取值范围.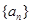 中,
中,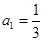 ,且前n项的算术平均数等于第n项的
,且前n项的算术平均数等于第n项的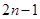 倍(
倍(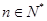 ).
). 满足
满足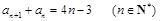 .
. 的值;
的值;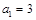 ,求数列
,求数列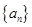 满足:
满足: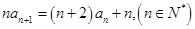 且
且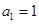 .
.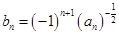 ,数列
,数列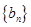 的前项和为
的前项和为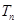 ,求证:
,求证: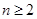 时,
时,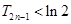 且
且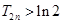
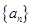 是首项为
是首项为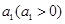 ,公差为
,公差为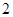 的等差数列,其前
的等差数列,其前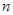 项和为
项和为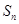 ,且
,且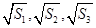 成等差数列.
成等差数列.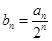 的前
的前 ,求
,求