Question

【题目】设点（a，b）是区域 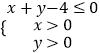内的任意一点，则使函数f（x）=ax2﹣2bx+3在区间[ ，+∞）上是增函数的概率为（ ）
A.
B.
C.
D.

Answer 1

【答案】A
【解析】解：作出不等式组对应的平面区域如图：若f（x）=ax2﹣2bx+3在区间[ ，+∞）上是增函数，
则 ，即 ，
则A（0，4），B（4，0），由 得 ，
即C（ ， ），
则△OBC的面积S= = ．
△OAB的面积S= 4=8．
则使函数f（x）=ax2﹣2bx+3在区间[ ，+∞）上是增函数的概率P= = ，
故选：A．

作出不等式组对应的平面区域，求出函数f（x）=ax2﹣2bx+3在区间[ ，+∞）上是增函数的等价条件，求出对应的面积，根据几何概型的概率公式进行求解即可．