题目内容
下列几个命题:①方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则a<0;
②函数y=
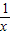 的单调递减区间是(-∞,0)∪(0,+∞);
的单调递减区间是(-∞,0)∪(0,+∞);③函数y=log2(x+1)+2的图象可由y=log2(x-1)-2的图象向上平移4个单位,向左平移2个单位得到;
④若关于x方程|x2-2x-3|=m两解,则m=0或m>4;
⑤函数f(x)=
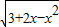 的值域是(0,2].
的值域是(0,2].其中正确的有 .
【答案】分析:①已知方程是一个二次函数,根据根与系数的关系,求出a的范围;
②根据反比例函数的图形和性质进行求解;
③根据对数函数的性质和平移的公式进行验证求解;
④我们根据对称变换图象的性质,我们易得方程|x2-2x-3|=m有两解时,m的取值范围,进而判断④的真假;
⑤根据根号有意义的条件先求出定义域,再根据配方法求出函数f(x)的值域;
解答:解:①中,若程x2+(a-3)x+a=0的有一个正实根,一个负实根
则x1•x2=a<0,故①正确;
②函数y=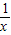 的单调递减区间是,(-∞,0),(0,+∞),故②错误;
的单调递减区间是,(-∞,0),(0,+∞),故②错误;
③y=log2(x-1)-2的图象向上平移4个单位,可得y=log2(x-1)-2+4=log2(x-1)+2,
向左平移2个单位得到y=log2(x+1)+2,故③正确;
④y=|x2-2x-3|的图象如图示: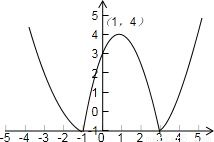
由图可知若关于x方程|x2-2x-3|=m有两解,则m=0或m>4,故④正确;
⑤函数f(x)=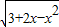 ,可得3+2x-x2≥0,可得-1≤x≤3,
,可得3+2x-x2≥0,可得-1≤x≤3,
∵3+2x-x2=-(x-1)2+4,可得x=1取最大值为4,
x=-1或3取得最小值为0,
∴函数f(x)=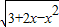 的值域是[0,2].
的值域是[0,2].
故⑤错误;
故答案为:①③④;
点评:本题考查的知识点有韦达定理,复合函数的定义域,函数图象的平移变换,函数的零点,函数的对称性,我们根据上述定义和概念,对五个结论逐一进行判断即可得到答案.
②根据反比例函数的图形和性质进行求解;
③根据对数函数的性质和平移的公式进行验证求解;
④我们根据对称变换图象的性质,我们易得方程|x2-2x-3|=m有两解时,m的取值范围,进而判断④的真假;
⑤根据根号有意义的条件先求出定义域,再根据配方法求出函数f(x)的值域;
解答:解:①中,若程x2+(a-3)x+a=0的有一个正实根,一个负实根
则x1•x2=a<0,故①正确;
②函数y=
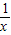 的单调递减区间是,(-∞,0),(0,+∞),故②错误;
的单调递减区间是,(-∞,0),(0,+∞),故②错误;③y=log2(x-1)-2的图象向上平移4个单位,可得y=log2(x-1)-2+4=log2(x-1)+2,
向左平移2个单位得到y=log2(x+1)+2,故③正确;
④y=|x2-2x-3|的图象如图示:

由图可知若关于x方程|x2-2x-3|=m有两解,则m=0或m>4,故④正确;
⑤函数f(x)=
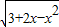 ,可得3+2x-x2≥0,可得-1≤x≤3,
,可得3+2x-x2≥0,可得-1≤x≤3,∵3+2x-x2=-(x-1)2+4,可得x=1取最大值为4,
x=-1或3取得最小值为0,
∴函数f(x)=
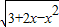 的值域是[0,2].
的值域是[0,2].故⑤错误;
故答案为:①③④;
点评:本题考查的知识点有韦达定理,复合函数的定义域,函数图象的平移变换,函数的零点,函数的对称性,我们根据上述定义和概念,对五个结论逐一进行判断即可得到答案.

练习册系列答案
相关题目