题目内容
已知![]() ,研究函数
,研究函数![]() 的单调区间。
的单调区间。
(1)当m=0时,f(x)的增区间为![]() 5分
5分
(2)当m≠0时,
①当![]() 在区间
在区间![]() 上是增函数;
上是增函数;
在区间![]() f(x)在此区间上是减函数;
f(x)在此区间上是减函数;
②![]() 在区间
在区间![]() 是减函数; 在区间
是减函数; 在区间![]() 是增函数;
是增函数;
③当m=3时, f(x)在(-![]() ,+
,+![]() )上是减函数;
)上是减函数;
④当m>3时,在区间![]() 是减函数, 在区间
是减函数, 在区间![]() 是增函数。
是增函数。
解析:
![]()
![]() 3分
3分
记![]() ∴只需讨论g(x)的正负即可。
∴只需讨论g(x)的正负即可。
(1)当m=0时,![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
∴当m=0时,f(x)的增区间为![]() 5分
5分
(2)当m≠0时,![]() 有两个根:
有两个根:![]()
①当![]()
在区间![]()
∴f(x)在此区间上是增函数;
在区间![]()
∴f(x)在此区间上是减函数; 7分
②![]()
在区间![]()
∴f(x)在此区间上是减函数;
在区间![]()
∴f(x)在此区间上是增函数; 9分
③当m=3时,![]()
在区间![]()
∵f(x)在x=-1处连续,
∴f(x)在(-![]() ,+
,+![]() )上是减函数; 11分
)上是减函数; 11分
④当m>3时,![]() ,
,
在区间![]()
∴f(x)在此区间上是减函数
在区间![]()
∴f(x)在此区间上是增函数。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
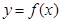 的图像(如图所示)过点
的图像(如图所示)过点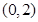 、
、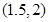 和点
和点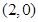 ,且函数图像关于点
,且函数图像关于点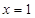 和
和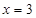 及
及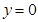 是它的渐近线.现要求根据给出的函数图像研究函数
是它的渐近线.现要求根据给出的函数图像研究函数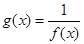 的相关性质与图像,
的相关性质与图像,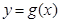 的定义域、值域及单调递增区间;
的定义域、值域及单调递增区间;
 的单调区间.
的单调区间. 的单调区间.
的单调区间.