题目内容
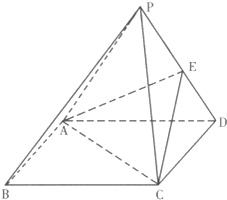 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,其中∠ADC=60°,侧面PAD丄底面ABCD,且PA=PD=3,E是PD的中点
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,其中∠ADC=60°,侧面PAD丄底面ABCD,且PA=PD=3,E是PD的中点(I)求证:直线PB∥平面ACE
(II)求:二面角E-AC-D的大小.
分析:(I) 设AC和BD的交点为O,可得OE是三角形DPB的中位线,OE∥PB,从而证得直线PB∥平面ACE.
(II)在平面PAD内,作EM⊥AD,作MN⊥AC,可证∠MNE即为二面角E-AC-D的平面角,求出EM和MN,可求
tan∠MNE,从的得到二面角E-AC-D的大小.
(II)在平面PAD内,作EM⊥AD,作MN⊥AC,可证∠MNE即为二面角E-AC-D的平面角,求出EM和MN,可求
tan∠MNE,从的得到二面角E-AC-D的大小.
解答:解:(I)证明:设AC和BD的交点为O,由菱形的性质可得,O为BD的中点,因为E是PD的中点,故OE是三角形DPB的中位线,
∴OE∥PB,而 OE?平面ACE,PB不在平面ACE内,故 直线PB∥平面ACE.
(II)在平面PAD内,作EM⊥AD,∵侧面PAD丄底面ABCD,∴EM⊥底面ABCD.作MN⊥AC,N为垂足,
则∠MNE即为二面角E-AC-D的平面角.
EM=
=
,MN=AMcos30°=
,∴tan∠MNE=
=
,
故二面角E-AC-D的大小为arctan
.
∴OE∥PB,而 OE?平面ACE,PB不在平面ACE内,故 直线PB∥平面ACE.
(II)在平面PAD内,作EM⊥AD,∵侧面PAD丄底面ABCD,∴EM⊥底面ABCD.作MN⊥AC,N为垂足,
则∠MNE即为二面角E-AC-D的平面角.
EM=
| 1 |
| 2 |
| 9-1 |
| 2 |
3
| ||
| 4 |
| EM |
| MN |
4
| ||
| 9 |
故二面角E-AC-D的大小为arctan
4
| ||
| 9 |
点评:本题考查证明线面平行的方法,直线和平面平行的判定,求二面角的大小的方法,找出二面角的平面角是解题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=