题目内容
在数列![]() .
.
(1)求证:数列![]() 是等差数列,并求数列
是等差数列,并求数列![]() 的通项公式
的通项公式![]() ;
;
(2)设![]() ,数列
,数列![]() 项和为
项和为![]() ,是否存在正整整m,使得
,是否存在正整整m,使得![]() 对于
对于![]() 恒成立,若存在,求出m的最小值,若不存在,说明理由.
恒成立,若存在,求出m的最小值,若不存在,说明理由.
解:(1)证明:![]()

![]() 数列
数列![]() 是等差数列 …………3分
是等差数列 …………3分
![]()
![]()
由![]()
![]() …………6
…………6
(2)![]()

![]() ………………10分
………………10分
依题意要使![]() 恒成立,只需
恒成立,只需![]()
解得![]() 所以m的最小值为1 ………………12分
所以m的最小值为1 ………………12分

练习册系列答案
相关题目
 。
。 是等差数列,并求数列
是等差数列,并求数列 的通项公式
的通项公式 ;
;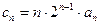 ,求数列
,求数列 的前
的前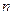 项和。
项和。 .
. 是等差数列,并求数列
是等差数列,并求数列 的通项公式
的通项公式 ;
; ,数列
,数列 项和为
项和为 ,是否存在正整整m,使得
,是否存在正整整m,使得 对于
对于 恒成立,若存在,求出m的最小值,若不存在,说明理由.
恒成立,若存在,求出m的最小值,若不存在,说明理由. .
. 是等差数列,并求数列
是等差数列,并求数列 的通项公式
的通项公式 ;
; ,数列
,数列 项和为
项和为 ,是否存在正整整m,使得
,是否存在正整整m,使得 对于
对于 恒成立,若存在,求出m的最小值,若不存在,说明理由.
恒成立,若存在,求出m的最小值,若不存在,说明理由. 。
。 是等差数列,并求数列
是等差数列,并求数列 的通项公式
的通项公式 ;
; ,求数列
,求数列 的前
的前 项和。
项和。 。
。 是等差数列,并求数列
是等差数列,并求数列 的通项公式
的通项公式 ;
; ,求数列
,求数列 的前
的前 项和。
项和。