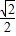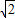题目内容
设n为自然数,a、b为正实数,且满足a+b=2,则
+
的最小值为( )
| 1 |
| 1+an |
| 1 |
| 1+bn |
A.
| B.
| C.1 | D.
|
| 1 |
| 1+an |
| 1 |
| 1+bn |
| an+bn+2 |
| (1+an)(1+bn) |
| (ab)n-1 |
| (1+an)(1+bn) |
要使
| 1 |
| 1+an |
| 1 |
| 1+bn |
| (ab)n-1 |
| (1+an)(1+bn) |
∵a、b为正实数,a+b=2,a+b≥2
| ab |
∵n为自然数,∴(ab)n-1≤1-1=0
当且仅当(ab)n=1时,(ab)n-1取得最大值0
∴a=b=1时,原式有最小值1.
故选C.

练习册系列答案
相关题目
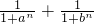 的最小值为
的最小值为


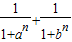 的最小值为( )
的最小值为( )
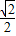
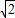
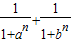 的最小值为( )
的最小值为( )