题目内容
已知三角形两边长分别为2和2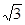 ,第三边上的中线长为2,则三角形的外接圆半径为
,第三边上的中线长为2,则三角形的外接圆半径为
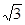 ,第三边上的中线长为2,则三角形的外接圆半径为
,第三边上的中线长为2,则三角形的外接圆半径为 2
分析:设AB=2,AC="2"
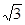 ,AD=2,D为BC边的中点,BC=2x,则BD=DC=x,由cos∠ADB=
,AD=2,D为BC边的中点,BC=2x,则BD=DC=x,由cos∠ADB=  ,cos∠ADC=
,cos∠ADC=  且cos∠ADB=-cos∠ADC,代入可求BC,则可得A=90°,外接圆的直径2R=BC,从而可求
且cos∠ADB=-cos∠ADC,代入可求BC,则可得A=90°,外接圆的直径2R=BC,从而可求解答:解:设AB=2,AC=2
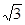 ,AD=2,D为BC边的中点,BC=2x,则BD=DC=x
,AD=2,D为BC边的中点,BC=2x,则BD=DC=x△ABD中,由余弦定理可得cos∠ADB=
 ,
,△ADC中,由余弦定理可得,cos∠ADC=

∴
 =-
=-
∴x=2
∴BC=4
∴AB2+AC2=BC2即A=90°
∴外接圆的直径2R=BC=4,从而可得R=2
故答案为:2

点评:本题主要考查了利用余弦定理求解三角形的应用,直角三角形的性质的应用,属于三角知识的综合应用.

练习册系列答案
相关题目
 的面积为
的面积为 ,
, ,则
,则 边上的高为( )
边上的高为( )



 中,
中, 分别为内角
分别为内角 的对边,且
的对边,且

 ,求
,求
 中,
中, ,
, ,
, .
. 的值;(Ⅱ)求
的值;(Ⅱ)求 的值.
的值.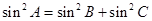 且,2cosB·sinC=sinA,则此三角形是( )
且,2cosB·sinC=sinA,则此三角形是( ) 、
、 、
、 为
为 的三内角,且其对边分别为
的三内角,且其对边分别为 、
、 、
、 ,若
,若 .
. ,求
,求 的周长等于
的周长等于 ,面积是
,面积是 ,
, ,则
,则 边的长是
边的长是



 ,若
,若 ,三角形面积为
,三角形面积为 ,
, ,则
,则 ( ▲ )
( ▲ )