题目内容
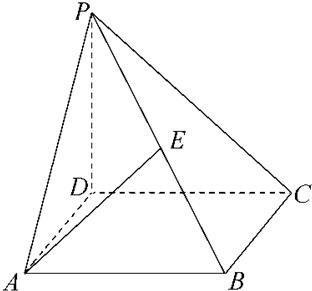 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=a,E是PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=a,E是PB的中点.
(1)求异面直线PD与AE所成角的正切值;
(2)在平面PAD内求一点F,使得EF⊥平面PBC;
(3)在(2)的条件下,求二面角F-PC-E的正切值.
解:(1)连接AC、BD交于点H,连接EH.
∵BH=DH,PE=EB,∴EH∥PD,
∴∠AEH为异面直线PD与AE所成的角,
∵EH= PD=
PD= ,
,
AH= AC=
AC= a,
a,
∴tan∠AEH= =
= ,即异面直线PD与AE所成角的正切值为
,即异面直线PD与AE所成角的正切值为 .
.
(2)设F为AD的中点,连接EF、HF.∵H、F分别为BD、AD的中点,∴HF∥AB,故HF⊥BC,又EH⊥BC,∴BC⊥平面EFH,因此BC⊥EF.

又PF2=PD2+DF2= a2,BF2=AB2+AF2=
a2,BF2=AB2+AF2= a2,
a2,
E为PB的中点,∴EF⊥PB.∴EF⊥平面PBC,即点F为AD的中点时满足题意.
(3)∵PD⊥平面ABCD,∴CD是PC在平面ABCD上的射影.
又CD⊥BC,∴PC⊥BC.取PC的中点G,连接EG,则EG∥BC,∴EG⊥PC,连接FG.
∵EF⊥平面PBC,∴EG是FG在平面PBC上的射影,且PC⊥EG,∴FG⊥PC.∴∠FGE为二面角F-PC-E的平面角,
∵EG= BC=
BC= ,
,
EF= =
=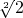 =
= a,
a,
∴tan∠FGE=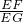 =
= ,
,
∴二面角F-PC-E的正切值为 .
.
分析:(1)连接AC、BD交于点H,连接EH,由EH∥PD,可得∠AEH为异面直线PD与AE所成的角,解三角形AEH即可得到异面直线PD与AE所成角的正切值;
(2)设F为AD的中点,连接EF、HF,由三角形的中位线定理可得HF∥AB,进而可得BC⊥平面EFH,则BC⊥EF,由勾股定理又可得到EF⊥PB,结合线面垂直的判定定理可得EF⊥平面PBC.
(3)由已知中PD⊥平面ABCD,由三垂线定理可得,PC⊥BC,取PC的中点G,连接EG,可得∠FGE为二面角F-PC-E的平面角,解三角形FGE即可得到二面角F-PC-E的正切值.
点评:本题考查的知识点是二面角的平面角及求法,异面直线及其所成的角,直线与平面垂直的判定,其中(1)(2)的关键是熟练掌握空间线线垂直,线面垂直,面面垂直之间的转换;(3)的关键是求出∠FGE为二面角F-PC-E的平面角.
∵BH=DH,PE=EB,∴EH∥PD,
∴∠AEH为异面直线PD与AE所成的角,
∵EH=
 PD=
PD= ,
,AH=
 AC=
AC= a,
a,∴tan∠AEH=
 =
= ,即异面直线PD与AE所成角的正切值为
,即异面直线PD与AE所成角的正切值为 .
.(2)设F为AD的中点,连接EF、HF.∵H、F分别为BD、AD的中点,∴HF∥AB,故HF⊥BC,又EH⊥BC,∴BC⊥平面EFH,因此BC⊥EF.

又PF2=PD2+DF2=
 a2,BF2=AB2+AF2=
a2,BF2=AB2+AF2= a2,
a2,E为PB的中点,∴EF⊥PB.∴EF⊥平面PBC,即点F为AD的中点时满足题意.
(3)∵PD⊥平面ABCD,∴CD是PC在平面ABCD上的射影.
又CD⊥BC,∴PC⊥BC.取PC的中点G,连接EG,则EG∥BC,∴EG⊥PC,连接FG.
∵EF⊥平面PBC,∴EG是FG在平面PBC上的射影,且PC⊥EG,∴FG⊥PC.∴∠FGE为二面角F-PC-E的平面角,
∵EG=
 BC=
BC= ,
,EF=
 =
=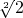 =
= a,
a,∴tan∠FGE=
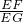 =
= ,
,∴二面角F-PC-E的正切值为
 .
.分析:(1)连接AC、BD交于点H,连接EH,由EH∥PD,可得∠AEH为异面直线PD与AE所成的角,解三角形AEH即可得到异面直线PD与AE所成角的正切值;
(2)设F为AD的中点,连接EF、HF,由三角形的中位线定理可得HF∥AB,进而可得BC⊥平面EFH,则BC⊥EF,由勾股定理又可得到EF⊥PB,结合线面垂直的判定定理可得EF⊥平面PBC.
(3)由已知中PD⊥平面ABCD,由三垂线定理可得,PC⊥BC,取PC的中点G,连接EG,可得∠FGE为二面角F-PC-E的平面角,解三角形FGE即可得到二面角F-PC-E的正切值.
点评:本题考查的知识点是二面角的平面角及求法,异面直线及其所成的角,直线与平面垂直的判定,其中(1)(2)的关键是熟练掌握空间线线垂直,线面垂直,面面垂直之间的转换;(3)的关键是求出∠FGE为二面角F-PC-E的平面角.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a, 如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点
如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点 (2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.
(2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.