题目内容
已知数列{an}满足:a1=1,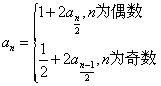 ,n=2,3,4,…,
,n=2,3,4,…,
(Ⅰ)求a3,a4,a5的值;
(Ⅱ)设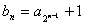 ,n=1,2,3,…,求证:数列{bn}是等比数列,并求出其通项公式;
,n=1,2,3,…,求证:数列{bn}是等比数列,并求出其通项公式;
(Ⅲ)对任意的m≥2,m∈N*,在数列{an}中是否存在连续的2m项构成等差数列?若存在,写出这2m项,并证明这2m项构成等差数列;若不存在,说明理由。
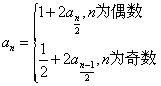 ,n=2,3,4,…,
,n=2,3,4,…,(Ⅰ)求a3,a4,a5的值;
(Ⅱ)设
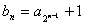 ,n=1,2,3,…,求证:数列{bn}是等比数列,并求出其通项公式;
,n=1,2,3,…,求证:数列{bn}是等比数列,并求出其通项公式;(Ⅲ)对任意的m≥2,m∈N*,在数列{an}中是否存在连续的2m项构成等差数列?若存在,写出这2m项,并证明这2m项构成等差数列;若不存在,说明理由。
解:(Ⅰ)因为a1=1,
所以a2=1+2a1=3,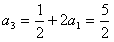 ,a4=1+2a2=7,
,a4=1+2a2=7,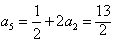 ;
;
(Ⅱ)证明:由题意,对于任意的正整数n,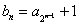 ,
,
所以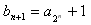 ,
,
又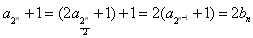 ,
,
所以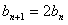 ,
,
又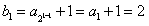 ,
,
所以{bn}是首项为2,公比为2的等比数列,
所以bn=2n;
(Ⅲ)存在。
事实上,对任意的m≥2,k∈N*,
在数列{an}中,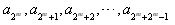 这连续的2m项就构成一个等差数列。
这连续的2m项就构成一个等差数列。
我们先来证明:“对任意的n≥2,n∈N*,k∈(0,2n-1),k∈N*,有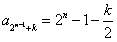 ”,
”,
由(Ⅱ),得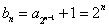 ,
,
所以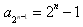 ,
,
当k为奇数时,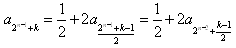 ,
,
当k为偶数时,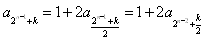 ,
,
记 ,
,
因此要证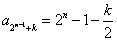 ,
,
只需证明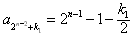 ,
,
其中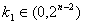 ,k1∈N*,
,k1∈N*,
(这是因为若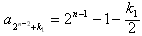 ,则当
,则当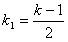 时,则k一定是奇数)
时,则k一定是奇数)
有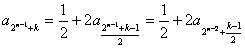
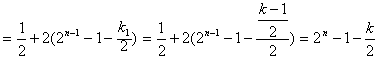 ;
;
当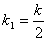 时,则k一定是偶数,
时,则k一定是偶数,
有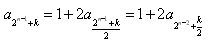
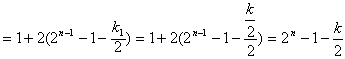 ,
,
如此递推,要证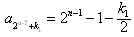 ,
,
只要证明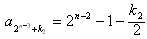 ,
,
其中 ,k2∈N*,
,k2∈N*,
如此递推下去,我们只需证明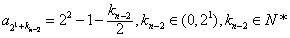 ,
,
即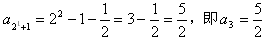 ,
,
由(Ⅱ)可得,所以对n≥2,n∈N*,k∈(0,2n-1),k∈N*,
有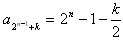 ,
,
对任意的m≥2,m∈N*,
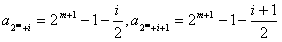 ,其中i∈(0,2m-1),i∈N*,
,其中i∈(0,2m-1),i∈N*,
所以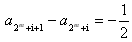 ,
,
又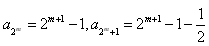 ,
,
所以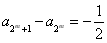 ,
,
所以 这连续的2m项,是首项为
这连续的2m项,是首项为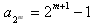 ,公差为
,公差为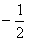 的等差数列。
的等差数列。
所以a2=1+2a1=3,
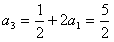 ,a4=1+2a2=7,
,a4=1+2a2=7,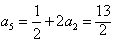 ;
;(Ⅱ)证明:由题意,对于任意的正整数n,
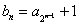 ,
,所以
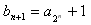 ,
,又
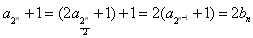 ,
,所以
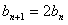 ,
,又
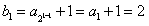 ,
,所以{bn}是首项为2,公比为2的等比数列,
所以bn=2n;
(Ⅲ)存在。
事实上,对任意的m≥2,k∈N*,
在数列{an}中,
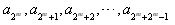 这连续的2m项就构成一个等差数列。
这连续的2m项就构成一个等差数列。我们先来证明:“对任意的n≥2,n∈N*,k∈(0,2n-1),k∈N*,有
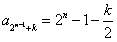 ”,
”,由(Ⅱ),得
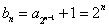 ,
,所以
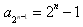 ,
,当k为奇数时,
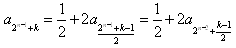 ,
,当k为偶数时,
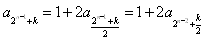 ,
,记
 ,
,因此要证
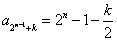 ,
,只需证明
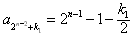 ,
,其中
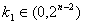 ,k1∈N*,
,k1∈N*,(这是因为若
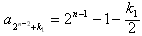 ,则当
,则当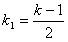 时,则k一定是奇数)
时,则k一定是奇数)有
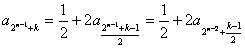
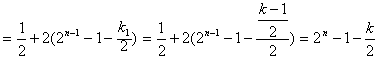 ;
;当
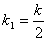 时,则k一定是偶数,
时,则k一定是偶数,有
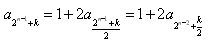
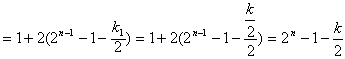 ,
,如此递推,要证
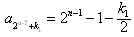 ,
,只要证明
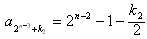 ,
,其中
 ,k2∈N*,
,k2∈N*,如此递推下去,我们只需证明
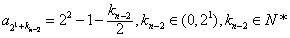 ,
,即
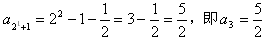 ,
,由(Ⅱ)可得,所以对n≥2,n∈N*,k∈(0,2n-1),k∈N*,
有
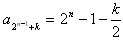 ,
,对任意的m≥2,m∈N*,
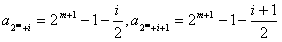 ,其中i∈(0,2m-1),i∈N*,
,其中i∈(0,2m-1),i∈N*,所以
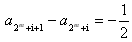 ,
,又
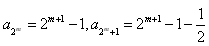 ,
,所以
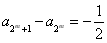 ,
,所以
 这连续的2m项,是首项为
这连续的2m项,是首项为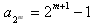 ,公差为
,公差为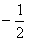 的等差数列。
的等差数列。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目