题目内容
 如图,边长为a的正三角形ABC,PA⊥平面ABC,PA=a,QC⊥平面ABC,QC=
如图,边长为a的正三角形ABC,PA⊥平面ABC,PA=a,QC⊥平面ABC,QC= ,PQ与AC延长线交于F点.
,PQ与AC延长线交于F点.
(1)若D为PB中点,证明:QD∥平面ABC;
(2)证明:BF⊥平面PAB.
 证明:(1)取AB中点E,连接DE,则DE
证明:(1)取AB中点E,连接DE,则DE
 PA,连接CE
PA,连接CE∵PA⊥面ABC,QC⊥面ABC,
∴PA∥QC,∴DE
 QC
QC∴四边形DECQ为矩形
∴DQ∥CE,CE?面ABC,
∴DQ∥面ABC(6分)
(2)∵PA∥QC,且

∴C为AF中点
∴BF⊥BA
∵PA⊥面ABC?BF⊥面PAB(11分)
∴BF⊥PA(12分)
分析:(1)取AB中点E,连接DE、CE,根据三角形中位线定理,及PA⊥面ABC,QC⊥面ABC,易证明出四边形DECQ为矩形,则DQ∥CE,由线面平行的判定定理,即可得到答案.
(2)由(1)中PA∥QC,PA=a,QC=
 ,易得到C为AF的中点,根据直角三角形性质,可得BF⊥BA,根据线面垂直的判定中得BF⊥面PAB.
,易得到C为AF的中点,根据直角三角形性质,可得BF⊥BA,根据线面垂直的判定中得BF⊥面PAB.点评:本题考查的知识点是直线与平面垂直的判定,直线与平面平行的判定,熟练掌握空间直线与平面平行及垂直的判定定理,几何特征是解答本题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
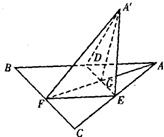 如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题:①动点A′在平面ABC上的射影在线段AF上;②三棱锥A′-FED的体积有最大值;③恒有平面A′GF⊥平面BCED;
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题:①动点A′在平面ABC上的射影在线段AF上;②三棱锥A′-FED的体积有最大值;③恒有平面A′GF⊥平面BCED; 如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有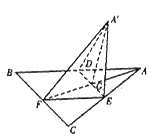
 线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有 (只需填上正确命题的序号).
线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有 (只需填上正确命题的序号). .
.
 线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有
(只需填上正确命题的序号).
线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有
(只需填上正确命题的序号). .
.