Question

函数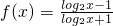，若f（x₁）+f（2x₂）=1（其中x₁，x₂均大于2），则f（x₁x₂）的最小值为________．

Answer 1

分析：设x₁=a，x₂=b，其中a、b均大于2，f（x）=1-，f（a）+f（2b）=2-2（）=1，所以能够推导出log₂2a+log₂4b≥8，所以log₂ab≥5，由此知f（ab）=1-≥．故f（x₁x₂）的最小值为．
解答：设x₁=a，x₂=b，其中a、b均大于2，
∵函数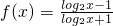，若f（a）+f（2b）=1，其中a＞2，b＞2．
f（x）=1-，
f（a）+f（2b）=2-2（）=1．
∴=．
由（log₂2a+log₂4b）（）≥4得
log₂2a+log₂4b≥8，
∴log₂ab≥5，
而f（ab）=1-≥．（等号当且仅当a=2b时成立）．
∴f（x₁x₂）的最小值为．
故答案为：．
点评：本题考查对数函数的性质和应用，解题时要认真审题，仔细解答，注意公式的合理运用．