题目内容
(12分)已知圆C1：
与圆C2：
相交于A、B两点。
⑴ 求公共弦AB的长；
⑵ 求圆心在直线
上，且过A、B两点的圆的方程；
⑶ 求经过A、B两点且面积最小的圆的方程。
【答案】
⑴
⑵
⑶
【解析】
试题分析：⑴由两圆方程相减即得
此为公共弦AB所在的直线方程
圆心
半径
C1到直线AB的距离为
故公共弦长
⑵ 圆心
，过C1，C2的直线方程为
，即
由
得所求圆的圆心为
它到AB的距离为
∴所求圆的半径为
∴所求圆的方程为
⑶ 过A、B且面积最小的圆就是以AB为直径的圆
由
，得圆心
半径
∴所求圆的方程为
考点：直线与圆相交的弦长及圆的标准方程
点评：直线与圆相交时圆的半径，圆心到直线的距离，弦长的一半构成直角三角形，第一问主要利用此三角形求解；第二问还可用待定系数法求方程
练习册系列答案
优等生题库系列答案
相关题目
，椭圆C2的方程为
，C2的离心率为
，如果C1与C2相交于A、B两点，且线段AB恰为圆C1的直径，试求：
的离心率为
，
与以原点为圆心、以椭圆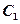
的短半轴长为半径的圆相切.
过点F1，且垂直于椭圆的长轴，动直线
垂直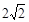
个单位沿射线OM方向运动，设运动时间为t秒.问：当t为何值时直线PQ与圆C1相切？
，椭圆C2的方程为
，C2的离心率为
，如果C1与C2相交于A、B两点，且线段AB恰为圆C1的直径，试求：（本小题满分12分）
已知椭圆C1和抛物线C2的焦点均在x轴上，C1的中心和C2的顶点均为原点，从它们每条曲线上至少取两个点，将其坐标记录于下表中：
|
x |
5 |
－ |
4 |
|
|
|
y |
2 |
0 |
－4 |
|
－ |
（Ⅰ）求C1和C2的方程；
（Ⅱ）过点S（0，－
）且斜率为k的动直线l交椭圆C1于A、B两点，在y轴上是否存在定点D，使以线段AB为直径的圆恒过这个点?若存在，求出D的坐标，若不存在，说明理由．