题目内容
偶函数f(x)=ax4+bx3+cx2+dx+e的图象过点P(0,1),且在x=1处的切线方程为y=x-2,则y=f(x)的解析式为分析:先根据f(x)的图象经过点(0,1)求出e,然后根据导数的几何意义求出函数f(x)在x=1处的导数,从而求出切线的斜率,建立一等量关系,再根据切点在曲线上建立一等式关系,解方程组即可.
解答:解:f(x)=ax4+bx3+cx2+dx+e的图象经过点(0,1),则e=1,
∵偶函数f(x)=ax4+bx3+cx2+dx+e,
故f(-x)=f(x)恒成立,
则b=d=0
即f(x)=ax4+cx2+e
f'(x)=4ax3+2cx,k=f'(1)=4a+2c=1(4分)
切点为(1,-1),则f(x)=ax4+cx2+1的图象经过点(1,-1),
得a+c+1=-1,得a=
,c=-
f(x)=
x4-
x2+1
故答案为:f(x)=
x4-
x2+1
∵偶函数f(x)=ax4+bx3+cx2+dx+e,
故f(-x)=f(x)恒成立,
则b=d=0
即f(x)=ax4+cx2+e
f'(x)=4ax3+2cx,k=f'(1)=4a+2c=1(4分)
切点为(1,-1),则f(x)=ax4+cx2+1的图象经过点(1,-1),
得a+c+1=-1,得a=
| 5 |
| 2 |
| 9 |
| 2 |
f(x)=
| 5 |
| 2 |
| 9 |
| 2 |
故答案为:f(x)=
| 5 |
| 2 |
| 9 |
| 2 |
点评:本题考查偶函数的性质,导数的计算与应用,注意导数计算公式的正确运用与导数与单调性的关系,利用导数研究曲线上某点切线方程,属于基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
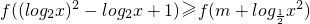 对任意x∈[2,4]恒成立,求实数m的取值范围.
对任意x∈[2,4]恒成立,求实数m的取值范围. 对任意x∈[2,4]恒成立,求实数m的取值范围.
对任意x∈[2,4]恒成立,求实数m的取值范围.