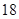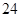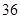题目内容
一个口袋里装有4个不同的红球,6个不同的白球,若取出一个红球记2分,取出一个白球记1分,从口袋中取出5个球,使总分低于7分的取法共有多少种?()
| A.186 | B.66 | C.60 | D.192 |
B
解析试题分析:解:设取x个红球,y个白球,于是: ,其中
,其中 ,
, 或
或 因此所求的取法种数是:
因此所求的取法种数是: (种),故选B.
(种),故选B.
考点:组合数公式.

练习册系列答案
相关题目
将9个相同的小球放入3个不同的盒子,要求每个盒子中至少有1个小球,且每个盒子中的小球个数都不相同,则共有不同的放法( )
| A.15种 | B.18种 | C.19种 | D.21种 |
编号为1、2、3、4、5的五个人分别去坐编号为1、2、3、4、5的五个座位,其中有且只有两个人的编号与座位号一致的坐法有( )种
| A.10种 | B.20种 | C.60种 | D.90种 |
从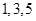 中选
中选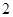 个不同数字,从
个不同数字,从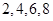 中选
中选 个不同数字排成一个五位数,则这些五位数中偶数的个数为( )
个不同数字排成一个五位数,则这些五位数中偶数的个数为( )
A.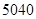 | B.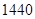 | C.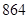 | D.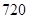 |
二项式 的展开式中常数项为( )
的展开式中常数项为( )
| A.-15 | B.15 | C.-20 | D.20 |
设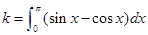 ,若
,若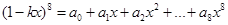 ,
,
则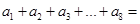 ( )
( )
| A.-1 | B.0 | C.l | D.256 |
设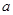 ,
,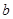 ,
,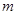 为整数(m>0),若
为整数(m>0),若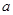 和
和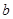 被
被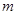 除得的余数相同,则称
除得的余数相同,则称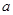 和
和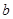 对模
对模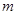 同余,记为
同余,记为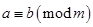 .若
.若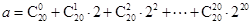 ,
,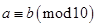 ,则
,则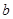 的值可以是( )
的值可以是( )
| A.2011 | B.2012 | C.2013 | D.2014 |
满足a,b∈{-1,0,1,2},且关于x的方程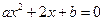 有实数解的有序数对(a,b)的个数为( )
有实数解的有序数对(a,b)的个数为( )
| A.14 |
| B.13 |
| C.12 |
| D.10 |