题目内容
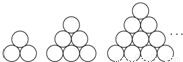
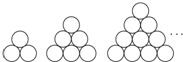 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有一层,就一个球,第2、3、4、…堆最底层(第一层)分别按下图所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=
在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有一层,就一个球,第2、3、4、…堆最底层(第一层)分别按下图所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=分析:由题意知f(1)=1,f(2)=f(1)+1+2,f(3)=f(2)+1+2+3,f(4)=f(3)+1+2+3+4,…f(n)=f(n-1)+1+2+3+4+…+n,利用累加法可求f(n)
解答:解析:易知f(3)=10.
由题意知f(2)比f(1)多最底层:1+2(个),
f(3)比f(2)多最底层:1+2+3(个),
f(4)比f(3)多最底层:1+2+3+4(个),
…
f(n)比f(n-1)多最底层:1+2+3++n(个),
∴f(n)-f(n-1)=1+2+3+…+n=
.
∴由累加法可得f(n)=
.
故答案为:10;
由题意知f(2)比f(1)多最底层:1+2(个),
f(3)比f(2)多最底层:1+2+3(个),
f(4)比f(3)多最底层:1+2+3+4(个),
…
f(n)比f(n-1)多最底层:1+2+3++n(个),
∴f(n)-f(n-1)=1+2+3+…+n=
| n(n+1) |
| 2 |
∴由累加法可得f(n)=
| n(n+1)(n+2) |
| 6 |
故答案为:10;
| n(n+1)(n+2) |
| 6 |
点评:本题主要考查数列求和在实际中的应用,解决问题的关键是先由f(1)、f(2)、f(3)的值通过归纳推理得到f(n)的表达式,在求和时注意累加法的运用.

练习册系列答案
相关题目

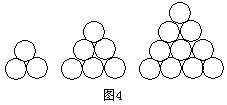 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干准“正三棱锥”形的展品,其中第一堆只有一层,
在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干准“正三棱锥”形的展品,其中第一堆只有一层,