题目内容
函数 是定义在实数集R上的奇函数,且当
是定义在实数集R上的奇函数,且当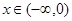 时,
时,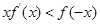 成立,若
成立,若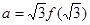 ,
,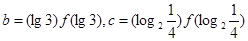 ,则
,则 大小关系( )
大小关系( )
A.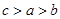 | B.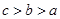 | C.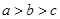 | D.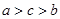 |
A
解析试题分析:函数 是定义在实数集R上的奇函数,
是定义在实数集R上的奇函数,
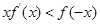 整理为
整理为 即
即
 是减函数
是减函数
考点:函数奇偶性单调性
点评:求解本题的入手点在于通过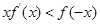 利用导数确定函数
利用导数确定函数 的单调性,进而通过单调性由自变量的大小得到函数值的大小
的单调性,进而通过单调性由自变量的大小得到函数值的大小

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数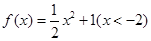 的反函数是
的反函数是
A.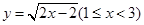 | B.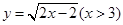 |
C.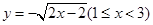 | D.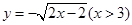 |
函数 的定义域是( )
的定义域是( )
| A.[-1,+∞) | B.[-1,0) | C.(-1,+∞) | D.(-1,0) |
已知 ,函数
,函数 的零点个数为
的零点个数为
| A.2 | B.3 | C.4 | D.2或3或4 |
如果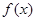 为偶函数,且
为偶函数,且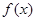 导数存在,则
导数存在,则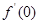 的值为 ( )
的值为 ( )
| A.2 | B.1 | C.0 | D.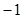 |
函数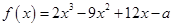 恰有两个不同的零点,则
恰有两个不同的零点,则 可以是( )
可以是( )
| A.3 | B.4 | C.6 | D.7 |
若关于 的方程
的方程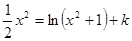 有四个不相等的实根,则实数
有四个不相等的实根,则实数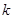 的取值范围是( )
的取值范围是( )
A.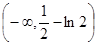 | B. | C.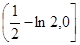 | D.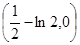 |
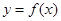 和
和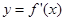 的图象画在同一个坐标系中,不可能正确的是( )
的图象画在同一个坐标系中,不可能正确的是( )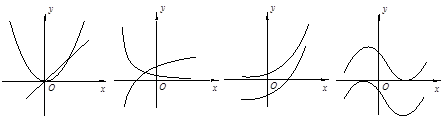
 (x>0)的图像经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为6,则k的值为【 】
(x>0)的图像经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为6,则k的值为【 】