题目内容
8．已知棱长为2的正方体ABCD-A1B1C1D1，球O与该正方体的各个面相切，则平面ACB1截此球所得的截面的面积为（ ）| A． | $\frac{8π}{3}$ | B． | $\frac{5π}{3}$ | C． | $\frac{4π}{3}$ | D． | $\frac{2π}{3}$ |
分析 求出平面ACB1截此球所得的截面的圆的半径，即可求出平面ACB1截此球所得的截面的面积．
解答 解：由题意，球心与B的距离为$\frac{1}{2}×2\sqrt{3}$=$\sqrt{3}$，B到平面ACB1的距离为$\frac{1}{3}×2\sqrt{3}$=$\frac{2\sqrt{3}}{3}$，球的半径为1，球心到平面ACB1的距离为$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$，∴平面ACB1截此球所得的截面的圆的半径为$\sqrt{1-\frac{1}{3}}$=$\sqrt{\frac{2}{3}}$，
∴平面ACB1截此球所得的截面的面积为$π•\frac{2}{3}$=$\frac{2π}{3}$，
故选D．
点评 本题考查平面ACB1截此球所得的截面的面积，考查学生的计算能力，属于中档题．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
满足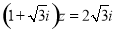
（
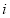为虚数单位），则
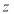在复平面内对应的点位于（ ）
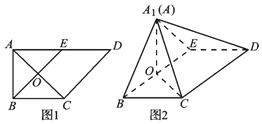如图1，在直角梯形ABCD中，AD∥BC，∠BAD=$\frac{π}{2}$，AB=BC=1，AD=2，E是AD的中点，O是AC与BE的交点．将△ABE沿BE折起到图22中△A1BE的位置，得到四棱锥A1-BCDE．
3．已知函数f（x）=x2ex+lnt-a，若对任意的t∈[1，e]，f（x）在区间[-1，1]总存在唯一的零点，则实数a的取值范围是（ ）
| A． | [1，e] | B． | $（1+\frac{1}{e}，e]$ | C． | （1，e] | D． | $[1+\frac{1}{e}，e]$ |
如图，三棱锥P-ABC中，PB⊥底面ABC，∠BCA=90°，PB=BC=CA=2，E为PC的中点，点F在PA上，且2PF=FA．
在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是一直角梯形，∠BAD=90°，AD∥BC，AB=BC=a，PA=$\frac{{2\sqrt{3}}}{3}$a，AD=2a．
如图，在四棱锥P-ABCD中，侧面PAB⊥底面ABCD，△PAB为正三角形．AB⊥AD，CD⊥AD，点E、M为线段BC、AD的中点，F，G分别为线段PA，AE上一点，且AB=AD=2，PF=2FA．