题目内容
(2012•闵行区一模)已知函数f(x)=|x+
|-|x-
|,关于x的方程f2(x)+a|f(x)|+b=0(a,b∈R)恰有6个不同实数解,则a的取值范围是
| 1 |
| x |
| 1 |
| x |
(-4,-2)
(-4,-2)
.分析:题中原方程f2(x)+a|f(x)|+b=0恰有6个不同实数解,故先根据题意作出f(x)的简图,由图可知,只有当f(x)=2时,它有二个根,且当f(x)=k(0<k<2),关于x的方程f2(x)+a|f(x)|+b=0(a,b∈R)恰有6个不同实数解,据此即可求得实数a的取值范围.
解答: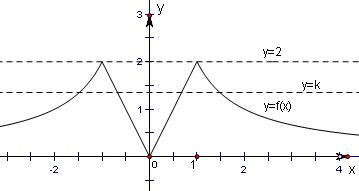 解:先根据题意作出f(x)的简图:
解:先根据题意作出f(x)的简图:
得f(x)>0.
∵题中原方程f2(x)+a|f(x)|+b=0(a,b∈R)恰有6个不同实数解,即方程f2(x)+af(x)+b=0(a,b∈R)恰有6个不同实数解,
∴故由图可知,只有当f(x)=2时,它有二个根.故关于x的方程f2(x)+af(x)+b=0中,
有:4+2a+b=0,b=-4-2a,
且当f(x)=k,0<k<2时,关于x的方程f2(x)+af(x)+b=0有4个不同实数解,
∴k2+ak-4-2a=0,
a=-2-k,∵0<k<2,
∴a∈(-4,-2).
故答案为:(-4,-2).
 解:先根据题意作出f(x)的简图:
解:先根据题意作出f(x)的简图:得f(x)>0.
∵题中原方程f2(x)+a|f(x)|+b=0(a,b∈R)恰有6个不同实数解,即方程f2(x)+af(x)+b=0(a,b∈R)恰有6个不同实数解,
∴故由图可知,只有当f(x)=2时,它有二个根.故关于x的方程f2(x)+af(x)+b=0中,
有:4+2a+b=0,b=-4-2a,
且当f(x)=k,0<k<2时,关于x的方程f2(x)+af(x)+b=0有4个不同实数解,
∴k2+ak-4-2a=0,
a=-2-k,∵0<k<2,
∴a∈(-4,-2).
故答案为:(-4,-2).
点评:数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.

练习册系列答案
相关题目
 (2012•闵行区一模)在一圆周上给定1000个点.(如图)取其中一点标记上数1,从这点开始按顺时针方向数到第二个点标记上数2,从标记上2的点开始按顺时针方向数到第三个点标记上数3,继续这个过程直到1,2,3,…,2012都被标记到点上,圆周上这些点中有些可能会标记上不止一个数,在标记上2012的那一点上的所有标记的数中最小的是
(2012•闵行区一模)在一圆周上给定1000个点.(如图)取其中一点标记上数1,从这点开始按顺时针方向数到第二个点标记上数2,从标记上2的点开始按顺时针方向数到第三个点标记上数3,继续这个过程直到1,2,3,…,2012都被标记到点上,圆周上这些点中有些可能会标记上不止一个数,在标记上2012的那一点上的所有标记的数中最小的是 (2012•闵行区一模)将边长分别为1、2、3、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.容易知道第1个阴影部分图形的周长为8.设前n个阴影部分图形的周长的平均值为f(n),记数列{an}满足
(2012•闵行区一模)将边长分别为1、2、3、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.容易知道第1个阴影部分图形的周长为8.设前n个阴影部分图形的周长的平均值为f(n),记数列{an}满足