题目内容
【题目】如图，已知曲线 
及曲线 
，C1上的点P1的横坐标为 
．从C1上的点 
作直线平行于x轴，交曲线C2于Qn点，再从C2上的点 
作直线平行于y轴，交曲线C1于Pn+1点，点Pn（n=1，2，3…）的横坐标构成数列{an}．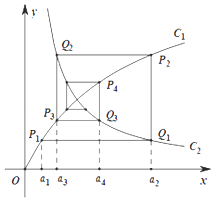 
（1）求曲线C1和曲线C2的交点坐标；
（2）试求an+1与an之间的关系；
（3）证明： 
．
【答案】
（1）解：∵曲线 
及曲线 
，
取立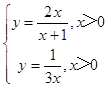 
，得x= 
，y= 
，
∴曲线C1和曲线C2的交点坐标是 
（2）解：设Pn（ 
）， 
，由已知 
，
又 
， 
= 
= 
= 
，
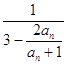（3）证明： an＞0，由 ， 
，
得 
与 
异号，
∵0＜a1
， 
， 
， 
，
∴a2n﹣1 
【解析】（1）取立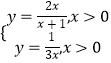 
，能求出曲线C1和曲线C2的交点坐标．（2）设Pn（ ）， ，由已知 ，能求出 ．（3）由 ， ，得 与 异号，由此能证明a2n﹣1 ．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
