题目内容
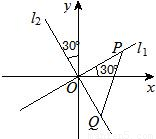
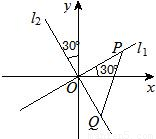
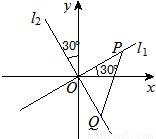
如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,已知线段PQ的长度为2,且点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动.(Ⅰ)求动点M(x1,x2)的轨迹C的方程;
(Ⅱ)设过定点T(0,2)的直线l与(Ⅰ)中的轨迹C交于不同的两点A、B,且∠AOB为锐角,求直线l的斜率k的取值范围.
【答案】分析:(Ⅰ)根据题意可知直线l1⊥l2,进而可求得两直线的方程,设出P,Q点的坐标分别代入直线方程,根据|PQ|=2求得 则动点M的轨迹方程可得.
则动点M的轨迹方程可得.
(Ⅱ)设出直线l的方程,带代入椭圆方程消去y,设A(x1,y1)、B(x2,y2),利用判别式求得k的范围,进而根据韦达定理表示出x1+x2和x1x2根据∵∠AOB为锐角,判断出 ,求得k的范围,最后综合取交集求得k的范围.
,求得k的范围,最后综合取交集求得k的范围.
解答: 解:(Ⅰ)由已知得直线l1⊥l2,l1:
解:(Ⅰ)由已知得直线l1⊥l2,l1: ,l2:
,l2:
∵P(x1,y1)在直线l1上运动,Q(x2,y2)直线l2上运动,
∴ ,
, ,
,
由|PQ|=2得(x12+y12)+(x22+y22)=4,
即 ,⇒
,⇒ ,
,
∴动点M(x1,x2)的轨迹C的方程为 .
.
(Ⅱ)直线l方程为y=kx+2,将其代入 ,
,
化简得(1+3k2)x2+12kx+9=0,
设A(x1,y1)、B(x2,y2)
∴△=(12k)2-36×(1+3k2)>0,⇒k2>1,
且 ,
,
∵∠AOB为锐角,∴ ,
,
即x1x2+y1y2>0,⇒x1x2+(kx1+2)(kx2+2)>0,
∴(1+k2)x1x2+2k(x1+x2)+4>0.
将 代入上式,
代入上式,
化简得 ,
, .
.
由k2>1且 ,得
,得 .
.
点评:本题主要考查了直线与圆锥曲线的综合问题.涉及到圆锥曲线的性质和直线的基本知识点,考查了基础知识的综合运用.
 则动点M的轨迹方程可得.
则动点M的轨迹方程可得.(Ⅱ)设出直线l的方程,带代入椭圆方程消去y,设A(x1,y1)、B(x2,y2),利用判别式求得k的范围,进而根据韦达定理表示出x1+x2和x1x2根据∵∠AOB为锐角,判断出
 ,求得k的范围,最后综合取交集求得k的范围.
,求得k的范围,最后综合取交集求得k的范围.解答:
 解:(Ⅰ)由已知得直线l1⊥l2,l1:
解:(Ⅰ)由已知得直线l1⊥l2,l1: ,l2:
,l2:
∵P(x1,y1)在直线l1上运动,Q(x2,y2)直线l2上运动,
∴
 ,
, ,
,由|PQ|=2得(x12+y12)+(x22+y22)=4,
即
 ,⇒
,⇒ ,
,∴动点M(x1,x2)的轨迹C的方程为
 .
.(Ⅱ)直线l方程为y=kx+2,将其代入
 ,
,化简得(1+3k2)x2+12kx+9=0,
设A(x1,y1)、B(x2,y2)
∴△=(12k)2-36×(1+3k2)>0,⇒k2>1,
且
 ,
,∵∠AOB为锐角,∴
 ,
,即x1x2+y1y2>0,⇒x1x2+(kx1+2)(kx2+2)>0,
∴(1+k2)x1x2+2k(x1+x2)+4>0.
将
 代入上式,
代入上式,化简得
 ,
, .
.由k2>1且
 ,得
,得 .
.点评:本题主要考查了直线与圆锥曲线的综合问题.涉及到圆锥曲线的性质和直线的基本知识点,考查了基础知识的综合运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
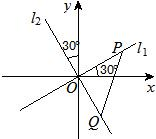 如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,已知线段PQ的长度为2,且点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动.
如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,已知线段PQ的长度为2,且点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动.