题目内容
已知点A是双曲线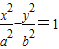 的右顶点,过点A且垂直于x轴的直线与双曲线的两条渐近线交于B、C两点,若△BOC为锐角三角形,则离心率的取值范围为 .
的右顶点,过点A且垂直于x轴的直线与双曲线的两条渐近线交于B、C两点,若△BOC为锐角三角形,则离心率的取值范围为 .
【答案】分析:为解题简单,可以设B在x轴上方,根据题意,若△BOC为锐角三角形,则∠BOA<45°,结合双曲线的渐近线方程进而可得KOB=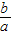 <1,而e2=
<1,而e2=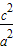 =
=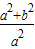 =1+
=1+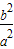 ,将
,将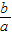 <1代入可得1<e2<2,进而开方可得答案.
<1代入可得1<e2<2,进而开方可得答案.
解答:解:设B在x轴上方,根据题意,若△BOC为锐角三角形,则∠BOA<45°,则KOB<1,
KOB=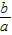 ,则
,则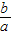 <1,
<1,
则e2=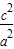 =
=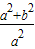 =1+
=1+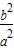 ,
,
易得1<e2<2,
则1<e<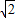 ,
,
故答案为(1,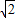 ).
).
点评:本题考查双曲线的简单性质,解题的关键是有△BOC为锐角三角形,得到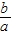 <1.
<1.
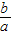 <1,而e2=
<1,而e2=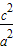 =
=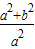 =1+
=1+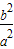 ,将
,将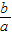 <1代入可得1<e2<2,进而开方可得答案.
<1代入可得1<e2<2,进而开方可得答案.解答:解:设B在x轴上方,根据题意,若△BOC为锐角三角形,则∠BOA<45°,则KOB<1,
KOB=
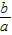 ,则
,则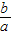 <1,
<1,则e2=
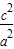 =
=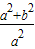 =1+
=1+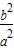 ,
,易得1<e2<2,
则1<e<
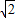 ,
,故答案为(1,
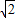 ).
).点评:本题考查双曲线的简单性质,解题的关键是有△BOC为锐角三角形,得到
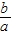 <1.
<1. 
练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 的右顶点,过点A且垂直于x轴的直线与双曲线的两条渐近线交于B、C两点,若△BOC为锐角三角形,则离心率的取值范围为________________.
的右顶点,过点A且垂直于x轴的直线与双曲线的两条渐近线交于B、C两点,若△BOC为锐角三角形,则离心率的取值范围为________________.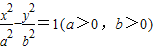 的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )
的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )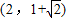
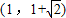
 的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )
的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )
