Question

已知双曲线=1(a＞0,b＞0)的右焦点为F₂，过F₂作渐近线的垂线，垂足为E，若|EF₂|=3，离心率e=2.

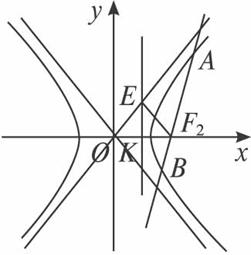
(1)求双曲线的方程；

(2)设双曲线的右准线与x轴相交于点K，过右焦点F₂任作一条直线l交双曲线右支于A(x₁,y₁),B(x₂,y₂)，求证:∠AKF₂=∠BKF₂.

Answer 1

答案：(1)解：根据题设条件设F₂(c,0)，双曲线的渐近线为y=±x，|EF₂|==b (∵a²+b²=c²),∴b=3.又e==2,∴a=1.

∴所求双曲线方程为x²=1.                                                

(2)证法一:易知F₂(2,0),当直线l与x轴垂直时，由对称性可知结论成立.

当直线l与x轴不垂直时，设l的方程为：y=k(x-2)，

由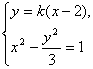消去y得(3-k²)x²+4k²x-4k²-3=0,则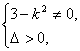则k²＞3，

要证∠AKF₂=∠BKF₂，只须证k_KA+k_KB=0，即 5(x₁+x₂)-4x₁x₂-4=0.①

又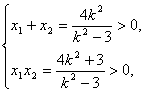①式成立.故命题成立.                                 

证法二:设A,B在右准线的射影为A′,B′,连结AK，BK，

由双曲线第二定义可知，

由平行线分线段成比例定理可知，

∴,

∴△AA′K∽△BB′K,∴∠AKA′=∠BKB′,

∴∠AKF₂=∠BKF₂.