题目内容
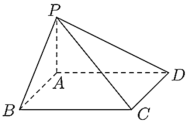
【题目】设四边形![]() 为矩形,点
为矩形,点![]() 为平面
为平面![]() 外一点,且
外一点,且![]() 平面
平面![]() ,若
,若![]() ,
,![]() .
.
(1)求![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(2)在![]() 边上是否存在一点
边上是否存在一点![]() ,使得点
,使得点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若点![]() 是
是![]() 的中点,在
的中点,在![]() 内确定一点
内确定一点![]() ,使
,使![]() 的值最小,并求此时
的值最小,并求此时![]() 的值.
的值.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)
;(3)![]() 、
、![]() 、
、![]() 三点共线,
三点共线,![]()
【解析】
(1)由题意可得:![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,可得
,可得![]() 与平面
与平面![]() 所成角既为
所成角既为![]() ,再利用解三角形的有关知识即可求出答案.
,再利用解三角形的有关知识即可求出答案.
(2)假设![]() 边上存在一点G满足题设条件,作
边上存在一点G满足题设条件,作![]() ,则
,则![]() 平面
平面![]() ,可得
,可得![]() ,进而得到
,进而得到![]() ,然后根据题意可得此点G符合题意.
,然后根据题意可得此点G符合题意.
(3)作出点C关于面PAB的对称点![]() ,连接
,连接![]() 交面PAB的点H,点H就是所求的点,再运用平面几何知识可求得HB的长.
交面PAB的点H,点H就是所求的点,再运用平面几何知识可求得HB的长.
(1)因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,又因为底面
,又因为底面![]() 是矩形,所以
是矩形,所以![]() ,
,
所以由线面垂直的判定定理可得:![]() 平面
平面![]() ,所以
,所以![]() 与平面
与平面![]() 所成角既为
所成角既为![]() ,
,
又由题意可得:![]() ,
,![]() ,所以
,所以![]() .
.
所以![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.
(2)假设![]() 边上存在一点G满足题设条件,作
边上存在一点G满足题设条件,作![]() ,
,
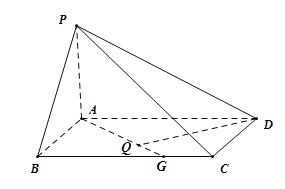
则![]() 平面
平面![]() ,
,
所以![]() .
.![]() ,
,
故存在点G,当![]() 时,使点D到平面
时,使点D到平面![]() 的距离为
的距离为![]() .
.
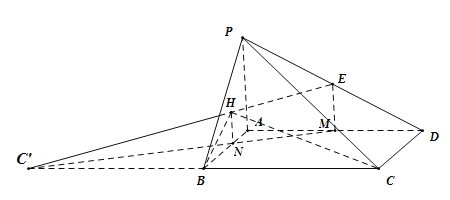
(3)延长CB到![]() ,使
,使![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为底面![]() 是矩形,
是矩形,
所以![]() ,
,
所以由线面垂直的判定定理可得:![]() 平面
平面![]() ,
,
则![]() 是点C关于面
是点C关于面![]() 的对称点,
的对称点,
连接![]() ,交面
,交面![]() 于H,
于H,
则点H是使![]() 的值最小时,在面
的值最小时,在面![]() 上的一点.
上的一点.
作![]() 于M,则点M是AD的中点,连接
于M,则点M是AD的中点,连接![]() 交AB于N,连接HN,
交AB于N,连接HN,
则![]() ,
,
所以![]() ,
,
又![]() ,
,
所以![]() ,而
,而![]() ,
,
所以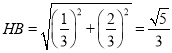 .
.
所以![]() .
.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目