题目内容
(本小题满分12分)
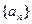 是首项
是首项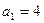 的等比数列,其前
的等比数列,其前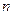 项和为Sn,且
项和为Sn,且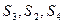 成等比数列.
成等比数列.
(1)求数列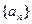 的通项公式;
的通项公式;
(2)若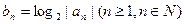 ,设
,设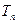 为数列
为数列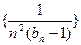 的前
的前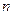 项和,
项和,
求证: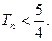
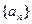 是首项
是首项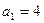 的等比数列,其前
的等比数列,其前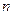 项和为Sn,且
项和为Sn,且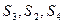 成等比数列.
成等比数列.(1)求数列
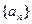 的通项公式;
的通项公式;(2)若
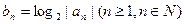 ,设
,设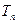 为数列
为数列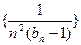 的前
的前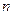 项和,
项和,求证:
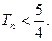
(1)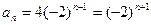
(2)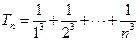
=1+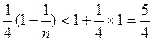
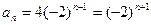
(2)
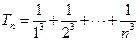
=1+
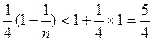
解:设数列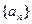 的公比为
的公比为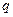
(1)若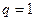 ,则
,则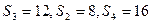
显然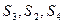 不成等差数列,与题设条件矛盾,所以
不成等差数列,与题设条件矛盾,所以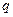 ≠1 1分
≠1 1分
由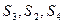 成等差数列,得
成等差数列,得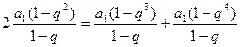
化简得 4分
4分
∴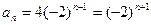 5分
5分
(2)解法1: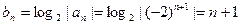 6分
6分
当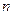 ≥2时,
≥2时,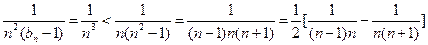
10分
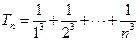

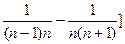
=1+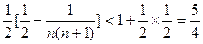 12分
12分
解法2: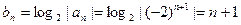 6分
6分
当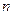 ≥2时,设
≥2时,设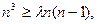 这里
这里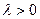 ,为待定常数.
,为待定常数.
则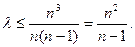
当n≥2时,易知数列 为单调递增数列,所以
为单调递增数列,所以
可见,n≥2时,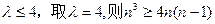
于是,n≥2时,有 10分
10分
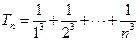
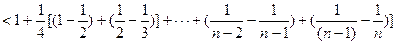
=1+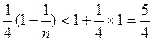 12分
12分
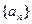 的公比为
的公比为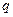
(1)若
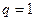 ,则
,则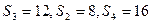
显然
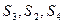 不成等差数列,与题设条件矛盾,所以
不成等差数列,与题设条件矛盾,所以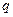 ≠1 1分
≠1 1分由
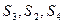 成等差数列,得
成等差数列,得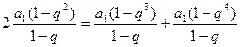
化简得
 4分
4分∴
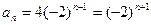 5分
5分(2)解法1:
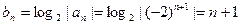 6分
6分当
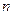 ≥2时,
≥2时,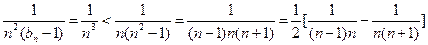
10分
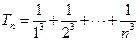

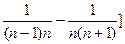
=1+
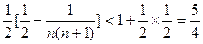 12分
12分解法2:
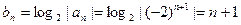 6分
6分当
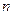 ≥2时,设
≥2时,设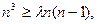 这里
这里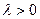 ,为待定常数.
,为待定常数.则
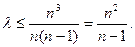
当n≥2时,易知数列
 为单调递增数列,所以
为单调递增数列,所以
可见,n≥2时,
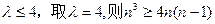
于是,n≥2时,有
 10分
10分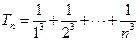
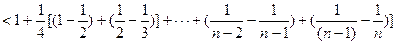
=1+
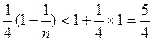 12分
12分
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
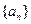 中,
中,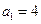 且对任意
且对任意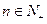 均有:
均有: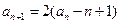
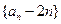 是等比数列;
是等比数列;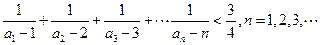
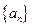 中,
中,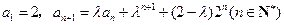 ,其中
,其中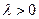 .
.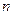 项和
项和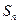 ;
;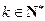 ,使得
,使得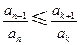 对任意
对任意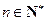 均成立.
均成立.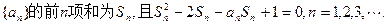
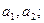
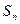 的表达式.
的表达式.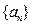 的通项公式是
的通项公式是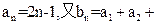 …+
…+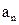
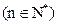
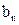 ;
;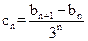 ,求数列
,求数列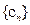 的前n项和.
的前n项和.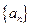 的各项均为正数,观察下面程序框图,
的各项均为正数,观察下面程序框图,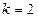 ;
;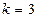 时,
时,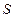 的表达式。
的表达式。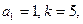 时,有
时,有 ,求数列
,求数列 ;
;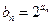 ,求
,求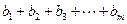 的
的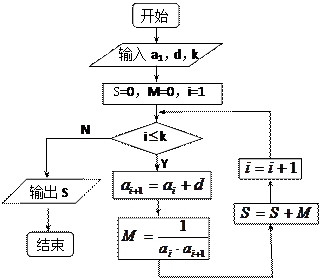
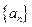 满足
满足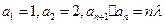 (
(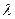 为常数,
为常数,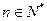 ),则
),则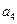 等于( )
等于( )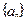 的前
的前 项和
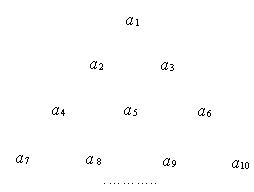
项和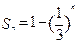 ,把
,把 行第
行第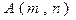
 ,则
,则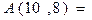 _____________.
_____________.
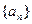 中,已知
中,已知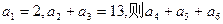 等于 ( )
等于 ( )