题目内容
若曲线
在点（a，f（a））处的切线与两条坐标轴围成的三角形的面积为18，则a=（ ）
|
| A． | 64 | B． | 32 | C． | 16 | D． | 8 |
A.
【解析】∵，（x＞0），
∴f'（x）=
，
∴在点（a，f（a））处的切线斜率k=f'（a）=
（a＞0）．
且f（a）=
，
∴切线方程为y﹣
=
（x﹣a），
令x=0，则y=
，
令y=0，则x=3a，即切线与坐标轴的交点坐标为（0，），（3a，0），
∴三角形的面积为
，
即
，
∴a=64．
故选：A．
练习册系列答案
导学全程练创优训练系列答案
相关题目
C.
D.
，AC=BD=
，AD=BC=
，则四面体ABCD的外接球的表面积为（ ）已知复数z满足z•i=2﹣i，i为虚数单位，则z的共轭复数
为（ ）
|
| A． | ﹣1+2 i | B． | l+2i | C． | 2﹣i | D． | ﹣1﹣2i |
设双曲线
﹣
=1（a＞0，b＞0）的右焦点为F，过点F作与x轴垂直的直线l交两渐近线于A、B两点，且与双曲线在第一象限的交点为P，设O为坐标原点，若
=λ
+μ
（λ，μ∈R），λμ=
，则该双曲线的离心率为（ ）
|
| A． |
| B． |
| C． |
| D． |
|
中，
. 
；
的余弦值；
上是否存在点
，使得平面
平面
，若存在，求出
的值；若不存在，请说明理由.
﹣
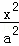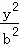=1（a＞0，b＞0）的右焦点为F，过点F作与x轴垂直的直线l交两渐近线于A、B两点，且与双曲线在第一象限的交点为P，设O为坐标原点，若
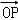=λ
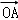+μ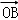
（λ，μ∈R），λμ=
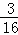，则该双曲线的离心率为（ ）
若
，则
的最大值为
时，
的值为（ ）
B．
C．
D．