Question

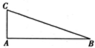
如图所示，在Rt△ABC中，∠CAB=90°，AB=2，AC=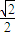．一曲线E过点C，动点P在曲线E上运动，且保持|PA|+|PB|的值不变，直线l经过A与曲线E交于M，N两点．
（1）建立适当的直角坐标系，求曲线E的方程；
（2）设直线l的斜率为k，若∠MBN为钝角，求k的取值范围．

Answer 1

【答案】分析：（1）以AB所在直线为x轴，AB的中点O为坐标原点，建立直角坐标系，确定P的轨迹为椭圆，即可求曲线E的方程；
（2）直线MN的方程为y=k（x+1），与椭圆方程联立，利用韦达定理，结合向量知识，即可得出结论．
解答：解：（1）以AB所在直线为x轴，AB的中点O为坐标原点，建立直角坐标系，则A（-1，0），B（1，0），
由题意，可得|PA|+|PB|=|CA|+|CB|=
∴P的轨迹为椭圆
设它的方程为（a＞b＞0），则a=，c=1
∴=1
∴椭圆的方程为；
（2）直线MN的方程为y=k（x+1），设M（x₁，y₁），N（x₂，y₂）
直线与椭圆方程联立，可得（1+2k²）x²+4k²x+2（k²-1）=0
∵△=8k²+8＞0
∴方程有两个不等的实数根
∴，
∴=（x₁-1，y₁），=（x₂-1，y₂）
∴=（x₁-1，y₁）•（x₂-1，y₂）=
∵∠MBN是钝角
∴，即
解得：
又M、B、N三点不共线
∴k≠0
综上所述，k的取值范围是．
点评：本题考查轨迹方程，考查直线与椭圆的位置关系，考查向量知识的运用，考查学生的计算能力，属于中档题．