题目内容
12.已知圆(x+2)2+y2=16的圆心为M,设A为圆上任一点,N(3,0),线段AN的垂直平分线交直线MA于点P,则动点P的轨迹是( )| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
分析 已知圆(x+2)2+y2=16,易知圆心和半径.A为圆上任一点和 N(2,0),线段AN的垂直平分线上任一点到两短点的距离相等且交MA于点P.有PN=PA,所以PM-PN=AM=4,即为动点P到两定点M、N的距离之差为常数4,根据双曲线的定义可得结论..
解答 解:已知圆(x+2)2+y2=16,则的圆心M(-2,0),半径为4.
A为圆上任一点,且AM=4
N(3,0),线段AN的垂直平分线上任一点到两端点的距离相等且交MA于点P.
有PN=PA
所以PM-PN=AM=4
即为动点P到两定点M、N的距离之差为常数4,
所以动点P的轨迹是双曲线.
故选:C.
点评 求点的轨迹方程常用的有定义法、待定系数法、直译法和间接法.其中定义法是最快捷的.这里就直接利用了双曲线的定义直接得到结论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.椭圆的一焦点与两顶点为等边三角形的三个顶点,则椭圆的长轴长是短轴长的( )
| A. | $\sqrt{3}$倍 | B. | 2倍 | C. | $\sqrt{2}$倍 | D. | $\frac{3}{2}$倍 |
3.已知点A(a,b)在y=-x2+3lnx的图象上,点B(m,n)在y=x+2的图象上,则(a-m)2+(b-n)2的最小值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 8 |
17.若直线ax-y+1=0与直线2x+y+2=0平行,则a的值为( )
| A. | -2 | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
4.下列函数中,定义域为[1,+∞)的是( )
| A. | y=$\sqrt{x-1}$+$\sqrt{x+1}$ | B. | y=(x-1)2 | C. | y=($\frac{1}{2}$)x-1 | D. | y=ln(x-1) |
1.圆锥SO的侧面展开图为如图所示的半径为4的半圆,半圆中∠ASC=45°.
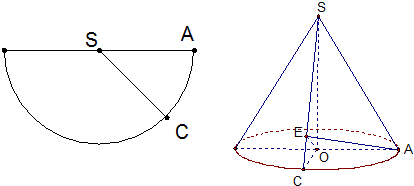
①圆锥SO的体积;
②在圆锥母线SC上是否存在一点E,使得SC⊥平面OEA,若存在,求此时SE~EC的值;若不存在,说明理由.

①圆锥SO的体积;
②在圆锥母线SC上是否存在一点E,使得SC⊥平面OEA,若存在,求此时SE~EC的值;若不存在,说明理由.
2.已知A(1,2,1),B(-1,3,4),C(1,1,1),$\overrightarrow{AP}$=2$\overrightarrow{PB}$,则$\overrightarrow{PC}$=( )
| A. | (-$\frac{1}{3}$,$\frac{8}{3}$,3) | B. | ($\frac{1}{3}$,-$\frac{8}{3}$,-3) | C. | (-$\frac{4}{3}$,$\frac{5}{3}$,2) | D. | ($\frac{4}{3}$,-$\frac{5}{3}$,-2) |