题目内容
已知函数f(x)=
sinx+cosx,g(x)=-x2+4x-3,对于?a∈[m,m+1],若?b∈[-
,0],满足g(a)=f(b),则m的取值范围是( )
| 3 |
| π |
| 3 |
A、[2-
| ||||
B、[1-
| ||||
C、[2-
| ||||
D、[1-
|
分析:求出函数f(x)在[-
,0]上的值域,利用g(a)=f(b)的关系求出g(a)的取值范围,利用二次函数的图象和性质,即可求出m的取值范围.
| π |
| 3 |
解答:解:f(x)=
sinx+cosx=2sin(x+
),
当b∈[-
,0],b+
∈[-
,
],
∴f(b)∈[-1,1],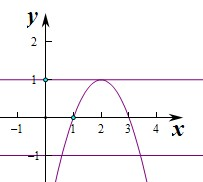
若g(a)=f(b),
∴g(a)∈[-1,1],
当g(x)=-x2+4x-3=1时,解得x=2,
当g(x)=-x2+4x-3=-1,即x2-4x+2=0,
解得x=2±
,
∴若-1≤g(a)≤1,
则2-
≤a≤2+
,
∵a∈[m,m+1],
∴
,
即
,
∴2-
≤m≤1+
,
故选:C.
| 3 |
| π |
| 6 |
当b∈[-
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∴f(b)∈[-1,1],

若g(a)=f(b),
∴g(a)∈[-1,1],
当g(x)=-x2+4x-3=1时,解得x=2,
当g(x)=-x2+4x-3=-1,即x2-4x+2=0,
解得x=2±
| 2 |
∴若-1≤g(a)≤1,
则2-
| 2 |
| 2 |
∵a∈[m,m+1],
∴
|
即
|
∴2-
| 2 |
| 2 |
故选:C.
点评:本题主要考查函数最值的应用,以及二次函数的图象和性质,利用数形结合是解决本题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知函数f(x)=3•2x-1,则当x∈N时,数列{f(n+1)-f(n)}( )
| A、是等比数列 | B、是等差数列 | C、从第2项起是等比数列 | D、是常数列 |