题目内容
在2014年3月15日,某超市对某种商品的销售量及其售价进行调查分析,发现售价x元和销售量y件之间的一组数据如下表所示:
| 售价x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
由散点图可知,销售量y与售价x之间有较好的线性相关关系,其线性回归方程是:y= -3.2x+a,则a=( )
A.-24 B.35.6 C.40.5 D.40
D
解析试题分析:线性回归方程必过样本中心点 ,
, ,
, ,代入线性回归方程得到
,代入线性回归方程得到 ,故选D.
,故选D.
考点:线性回归方程

练习册系列答案
相关题目
为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为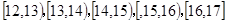 ,将其按从左到右的顺序分别编号为第一组,第二组,……,第五组,右图是根据试验数据制成的频率分布直方图。已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
,将其按从左到右的顺序分别编号为第一组,第二组,……,第五组,右图是根据试验数据制成的频率分布直方图。已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )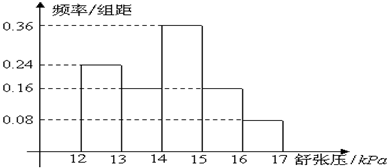
| A.6 | B.8 | C.12 | D.18 |
一个样本数据按从小到大的顺序排列为: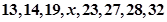 ,其中,中位数是
,其中,中位数是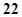 ,则
,则 等于( )
等于( )
A.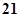 | B.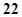 | C.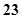 | D.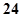 |
设某大学的女生体重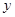 (单位:
(单位: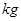 )与身高
)与身高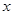 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据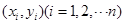 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为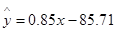 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.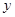 与 与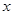 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心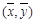 |
| C.若该大学某女生身高增加lcm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系,随机抽查52名中学生,得到统计数据如表1至表4,这与性别有关联的可能性最大的变量是( )
| 表1 | 不及格 | 及格 | 总计 |
| 男 | 6 | 14 | 20 |
| 女 | 10 | 22 | 32 |
| 总计 | 16 | 36 | 52 |
| 表2 | 不及格 | 及格 | 总计 |
| 男 | 4 | 16 | 20 |
| 女 | 12 | 20 | 32 |
| 总计 | 16 | 36 | 52 |
| 表3 | 不及格 | 及格 | 总计 |
| 男 | 8 | 12 | 20 |
| 女 | 8 | 24 | 32 |
| 总计 | 16 | 36 | 52 |
| 表4 | 不及格 | 及格 | 总计 |
| 男 | 14 | 6 | 20 |
| 女 | 2 | 30 | 32 |
| 总计 | 16 | 36 | 52 |
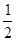 ,1),倾斜角
,1),倾斜角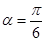 ,在极坐标系下,圆C的极坐标方程为
,在极坐标系下,圆C的极坐标方程为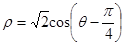 。
。
 )
)